Genesis
- 11
- 0
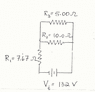
Hi, I need help with an electricity question where it requires for me to see the circuit diagram and figure out: volage drop across the resistor (V), current flowing through the resistor (I), the resistance constant (R).
Here is the link to the diagram that I've scanned:
http://gallery.cybertarp.com/albums/userpics/12541/electricity.gif
Basically, I need to figure out all the V, I and R for each resistor,
so basically I need to figure out everything, which are...
R1, R2, R3, Rt (total), I1, I2, I3, It (total), V1, V2, V3 and Vt (total)
I thought I could find Rt by using the equation:
Rt = R1 + R2 + R3 or 1/Rt = 1/R1 + 1/R2 + 1/R3, but none of those work. I think the only way to start this question is to figure out Rt first.
By the way, the answers are:
It = 12A
Rt = 11 ohms
Vt = 132V
I1 = 12A
R1 = 7.67 ohms
V1 = 92V
I2 = 4A
R2 = 10 ohms
V2 = 40V
I3 = 8A
R3 = 5 ohms
V3 = 40V
I greatly appreciate your help. Thanks in advance!
Here is the link to the diagram that I've scanned:
http://gallery.cybertarp.com/albums/userpics/12541/electricity.gif
Basically, I need to figure out all the V, I and R for each resistor,
so basically I need to figure out everything, which are...
R1, R2, R3, Rt (total), I1, I2, I3, It (total), V1, V2, V3 and Vt (total)
I thought I could find Rt by using the equation:
Rt = R1 + R2 + R3 or 1/Rt = 1/R1 + 1/R2 + 1/R3, but none of those work. I think the only way to start this question is to figure out Rt first.
By the way, the answers are:
It = 12A
Rt = 11 ohms
Vt = 132V
I1 = 12A
R1 = 7.67 ohms
V1 = 92V
I2 = 4A
R2 = 10 ohms
V2 = 40V
I3 = 8A
R3 = 5 ohms
V3 = 40V
I greatly appreciate your help. Thanks in advance!
Attachments
Last edited: