Rugile
- 79
- 1
Homework Statement
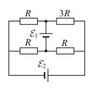
In the circuit (see attachment) we have 2 sources. If we decrease the EMF of the first source (ε1) by 1.5V, the current changes in every branch of the circuit. How does the EMF of the source ε2 has to be changed, so that the current through the ε1 source would be the same as previously?
Homework Equations
Kirchhoff's laws
The Attempt at a Solution
I guess what we need to do here is to find the dependency of ε1 on ε2. Is using the Kirchhoff's equations the best way here? I wrote down such eq:
<br /> I_3R + I_1r_1 + I_5R = \epsilon_1<br />
<br /> 3I_4R + I_6R + I_1r_1 = \epsilon_1<br />
<br /> I_2r_2 + I_6R - I_5R = \epsilon_2<br />
<br /> I_3 + I_4 = I_1<br />
<br /> I_5+I_6 = I_1<br />
<br /> I_3 = I_5 + I_2<br />
<br /> I_4 + I_2 = I_6<br />
Here r1, r2 - internal resistances of the sources (since there is current flowing through the sources, they must have internal resistances, right?)
I3 - top left resistor
I5 - down left resistor
I4 - top right resistor
I6 - down right resistor
I1 - ε1 current
I2 - ε2 current
But couldn't solve the system :/
Maybe there is a better way to do this? It seems to me there should be something simpler than system of 8 equations?
Any help appreciated!