baby_1
- 159
- 16
Hello
I have some problems to obtaining Electromagnetic density via Ampere's Law.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/indtor.html
my problem is why we don't calculate and sum Inflow and outflow of Ampere's closed loop path.to clearing my question please take a look at below picture.
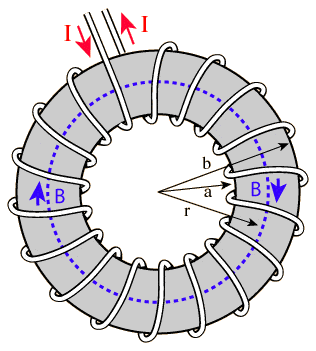
in upper side of Toroid current direction is going into center of Ampere's closed loop path however down side current direction is going out subsequently input current and output current in Ampere's closed loop path should be zero.
what is my misunderstand?
Thanks
I have some problems to obtaining Electromagnetic density via Ampere's Law.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/indtor.html
my problem is why we don't calculate and sum Inflow and outflow of Ampere's closed loop path.to clearing my question please take a look at below picture.
in upper side of Toroid current direction is going into center of Ampere's closed loop path however down side current direction is going out subsequently input current and output current in Ampere's closed loop path should be zero.
what is my misunderstand?
Thanks