Electron entering a magnetic field

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

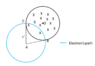
At any instant in the circular region, let the horizontal and vertical components of velocity of electron be $v_x$ and $v_y$. Let the origin be at the point from where the electron enters the magnetic field. Positive x-axis is in horizontal direction to left and positive y-axis in vertically upward direction.

The force acting on the electron is
F=q\vec{v}\times \vec{B}
F=q(v_x\hat{i}+v_y\hat{j}) \times (B\hat{-k})
\Rightarrow F=qv_yB\hat{i}+qv_xB\hat{j}

From the above equation, $dv_x/dt=qv_yB$ and $dv_y/dt=qv_xB$
As $v_x^2+v_y^2=v^2$, hence $v_xdv_x=-v_ydv_y$. If I substitute for $dv_x$ and $dv_y$, I end up proving $1=1$.

Any help is appreciated. Thanks!

 

[Sunil Simha]

Since you are given the speed of the electron, you can find the radius of curvature of its path (and hence the equation of the circular path). Then you can find the length of the path inside the field and calculate the time taken to travel.

 

[Saitama]

Since you are given the speed of the electron, you can find the radius of curvature of its path (and hence the equation of the circular path).

Do you want me to set up a coordinate system, make equation for the two circles and calculate the arc length? Wouldn't that be too dirty?

r'=\frac{mv}{eB}
$r'$ is the radius of curvature for the electron's path.

 

[TSny]

Do you want me to set up a coordinate system, make equation for the two circles and calculate the arc length? Wouldn't that be too dirty?

Draw a sketch of the trajectory passing through the B-field region. Mark the center of the circular trajectory. See if you can construct some triangles that will allow you to find the angle (with vertex at the center of the trajectory) subtended by the arc of the trajectory inside the B-field region. You won't need to introduce a coordinate system or solve simultaneous equations.

 

[Saitama]

Draw a sketch of the trajectory passing through the B-field region. Mark the center of the circular trajectory. See if you can construct some triangles that will allow you to find the angle (with vertex at the center of the trajectory) subtended by the arc of the trajectory inside the B-field region. You won't need to introduce a coordinate system or solve simultaneous equations.

I still have got no idea. :(
See attachment for the sketch of trajectory.
(The trajectory won't be a circular path outside the magnetic field.)

 

[TSny]

You need angle CAB. Construct triangles AOC and AOB.

 

[haruspex]

... and consider what angle ACO is.

 

[Saitama]

You need angle CAB. Construct triangles AOC and AOB.

... and consider what angle ACO is.

That was really obvious. Why I couldn't think of it. :P

Thank you both, I have got the right answer.