Electrostatic Force curved beam

Click For Summary
SUMMARY

The discussion focuses on calculating the electrostatic force between a curved beam and a standard parallel plate electrode. The user possesses an equation for the critical force required to induce snapping between bi-stable states of the beam but seeks guidance on deriving the electrostatic force in this specific configuration. It is noted that while the electrostatic force for two parallel plates is understood, the complexity increases with the curvature of the beam. The user emphasizes the relevance of the infinite plate electric field, which remains constant regardless of distance.

PREREQUISITES
  • Understanding of electrostatic force calculations
  • Familiarity with bi-stable beam mechanics
  • Knowledge of parallel plate electrode configurations
  • Basic principles of electric fields and their behavior
NEXT STEPS
  • Research methods for calculating electrostatic forces in non-linear geometries
  • Explore the principles of curved beam mechanics in electrostatics
  • Study the effects of electric field variations on curved surfaces
  • Investigate advanced topics in electrostatic actuation and stability analysis
USEFUL FOR

Mechanical engineers, electrical engineers, and researchers working on electrostatic actuation systems or studying the mechanics of curved beams in electrostatic fields.

Chase_md
Messages
1
Reaction score
0
Hi,

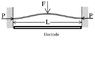
I'm trying to figure out what the electrostatic force between a curved beam (see picture attached) and a standard parallel plate electrode would be. I have an equation for the critical force to induce snapping between the bi-stable states of the beam, but I need to find out one for electrostatic force to induce this snapping.

I know how to obtain the electrostatic force for 2 parallel plates, but when the beam is curved I'm having an issue. Can someone point me in the right direction here?

Thanks so much!
 

Attachments

  • beam.png
    beam.png
    5.6 KB · Views: 485
Physics news on Phys.org
For infinite plate electric field does not depend on distance.
 

Similar threads

Electrostatics - Charged Plate Force Calculator
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad When to properly use "voltage"
  • · Replies 25 ·
Replies
25
Views
2K
Point charge with very thin metal sheet along a spherical surface
  • · Replies 21 ·
Replies
21
Views
2K
High School What is the *truth* of the electrostatic force
  • · Replies 15 ·
Replies
15
Views
4K
Undergrad Apparent Weight problem (falling beam)
  • · Replies 2 ·
Replies
2
Views
2K
High School Beam on an inclined plane
  • · Replies 4 ·
Replies
4
Views
958
What Is the Electrostatic Force Between an Ideal Dipole and a Conducting Plate?
  • · Replies 1 ·
Replies
1
Views
3K
Potential energy due to an external charge and a grounded sphere
  • · Replies 8 ·
Replies
8
Views
9K
Equivalent system (force+couple moment) of a loaded beam
  • · Replies 9 ·
Replies
9
Views
3K
Undergrad Why Is the Exerted Force Equal and Opposite to the Electrostatic Force?
  • · Replies 3 ·
Replies
3
Views
1K