Energy and Entropy from P-V Diagram

[Rapier]

Homework Statement

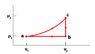
An ideal monatomic gas is taken through the above cycle where p1= 2 X 105 Pa and V1 = 5 cm3. During the cycle both the pressure and volume will change such that p2 = 2 p1 and V2 = 4 V1.

a) How much work is done by the gas in going from state a to state c along path abc?
Wabc = 3 J
OK

b) What is the change in internal energy in going from b to c?
Ubc= J

c) What is the change in internal energy during the complete cycle?
UTOT = 0 J
OK

d) What is the change in entropy per mole of gas in going from b to c?
ΔSbc = J/K

e) What is the change in entropy per mole during the complete cycle?
ΔSTOT= 0 J/K
OK

I am having problems with Parts B and D.

Homework Equations

PV=NRT
Q = nCvdt

The Attempt at a Solution

I only have P and V. I cannot use the Ideal Gas Law to calculate n or T because I have two unknowns. I cannot use my Heat Equations because I am still missing n and T. I'm just stuck. If I can calculate B, I think I can get D...I just don't see any way to calculate the Heat in part B. HELP!

Thanks.

 

[Andrew Mason]

b) What is the change in internal energy in going from b to c?
Ubc= J

Use: ΔU = nCvΔT = n(3R/2)ΔT

Since PV = nRT, you can express ΔT in terms of ΔP and V (V is constant).

d) What is the change in entropy per mole of gas in going from b to c?
ΔSbc = J/K

Use: dS = dQ/T. What is the heat flow in terms of dT and Cv? Integrate that to get ΔS.

AM

 

[Rapier]

Use: ΔU = nCvΔT = n(3R/2)ΔT

Since PV = nRT, you can express ΔT in terms of ΔP and V (V is constant).

Use: dS = dQ/T. What is the heat flow in terms of dT and Cv? Integrate that to get ΔS.

I can't believe I didn't see that. Once I read "express ΔT in terms of ΔP and V" it all fell together. It took me less than 2 minutes to solve the problems. Thanks! :)