- #1
KateyLou
- 17
- 0
Homework Statement
I have coursework on rhe convolution integral, however i am struggling to find the equation of motion to start the whole thing off with.
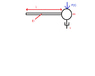
I will attach a picture of the problem, is is simply a cantilevered bar with a concentrated mass on the end and a damper.
Homework Equations
I am assuming you find the deflection at the end of the beam as a result of the force P(t), which i think is
P(t)L^3/3EI
However i am not sure where to go from here
The Attempt at a Solution
Thinking it may possibly be
m[tex]\ddot{x}[/tex]+c[tex]\dot{x}[/tex]=P(t)L^3/3EI
however i think i may need to add in stiffness somewhere else..