- #1
silentwf
- 37
- 0
Homework Statement
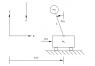
The nonlinear, inherently unstable inverted pendulum is shown in
Figure 1.15. The goal is to maintain the pendulum angle θ(t) = 0
by using a feedback controller with a sensor (encoder or poten-
tiometer) for θ(t) and an actuator to produce an input force f (t).
The cart mass is m 1 , the pendulum point mass is m 2 , and we
assume that the pendulum rod is massless. There are two possi-
ble outputs, the pendulum angle θ(t) and the cart displacement
w(t). The classical inverted pendulum has only one input, the
force f (t). We will consider a second case, using a motor to
provide a second input τ(t) (not shown) at the rotary joint of
Figure 1.15. For both cases (they will be very similar), derive the
nonlinear model for this system, i.e., draw the free-body diagrams
and write the correct number of independent ordinary differential
equations.
(See attached file for picture)
Homework Equations
[itex]\Sigma F = ma[/itex]
The Attempt at a Solution
So I only want to ask a concept question and not the whole solution. My question is in the derivation of the equation of motion. I referenced http://www.spumone.org/courses/control-notes/inverted-pendulum/ for an equation of motion, but I have one question. In the derivation of the equation, the author of the video combines the x and y components and solves for the entire system. My question is, can I solve only for the part X?
Here's what I did: (i used mb to signify mass of ball point, mc to signify mass of cart)
Looking at only the cart:
in the x direction [itex](m_{c}+m_{b})\ddot{w_{cart}}=f-T\sin{\theta}[/itex]
Looking only at the point mass:
in the x direction [itex]T\cdot\sin{\theta}=f-m_{c}\cdot \ddot{w_{cart}} = -m_{b}L\ddot{\theta}\cos{\theta}-m_{b}L\dot{\theta}^{2}\sin{\theta}[/itex]
Since the Tension forces must equate on the point mass and on the cart, combining two equations give us:
[itex](m_{c}+m_{b})\ddot{w_{cart}}=f+ m_{b}L\ddot{\theta}\cos{\theta} + m_{b}L\dot{\theta}^{2}\sin{\theta}[/itex]
Now my question is, can I use this to derive my nonlinear model and use this as state space equations?
Also, in the case that I have theta as a function of cosine/sine, how would I express my state-space?
Attachments
Last edited: