Mechanical Vibrations - 2 DOF System - Rod with 2 springs

[Master1022]

Homework Statement

Derive equations of motion in terms of the displacements $x_1$ and $x_2$

Relevant Equations

F = ma

Hi,

So the question is to: derive the equations of motion for the following in terms of x1 and x2? The bar is assumed to be light and rigid.

(NB. I know I posted another vibrations problem earlier in which I tried to use an energy approach to get to the equations of motion. However, we haven't been taught these, so I believe we are expected to reach these solutions by using force methods)

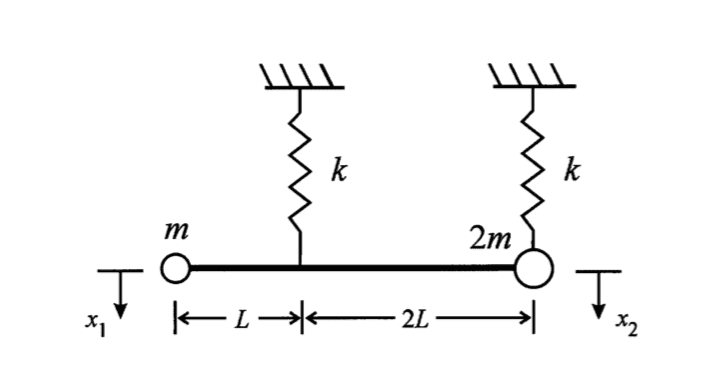
I am just wondering whether there is a general method when approaching these 2-DOF vibration problems? (e.g. introduce another variable for equations, specific places to take moments about, etc). I was wondering whether my method seems correct?

1) Resolve vertically downwards
I have decided to define an angle $\theta$ in the CCW direction from the point where the 2m mass is so that $\theta = \frac{x_1 - x_2}{3L}$

Also, I have identified that the COM is L away from the 2m mass. I have also made small angle approximations for the angles.

Therefore, we get the following when we resolve vertically downwards and get:
$$-k x_2 - k \left( x_2 + 2L \theta \right) = m \left( \ddot x_2 + L \ddot \theta \right)$$
rearranging and substituting in for $\ddot \theta$ leads to:
$$m \ddot x_1 + 2m \ddot x_2 + 2k x_1 + 4k x_2 = 0$$

2) Take moments about the centre of mass CCW direction
Because the bar is assumed to be rigid, I thought that the angle $\theta$ will be the same at the COM as it is at the right side

Taking moments, I get:
$$k x_2 L - 2mgL + mg(2L) - k \theta L^2 = I \ddot \theta$$
noting that: $I = m(2L)^2 + 2m(L)^2 = 6mL^2$ and rearranging we get:
$$6m \ddot x_1- 6m \ddot x_2 + 4k x_1 - 4k x_2 = 0$$

Combining these into matrix form, we get:
$$\begin{bmatrix} m & 2m \\ 6m & -6m \end{bmatrix} \begin{bmatrix} \ddot x_1 \\ \ddot x_2 \end{bmatrix} + \begin{bmatrix} 2k & 4k \\ 4k & -4k \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 0$$

Does this equation look correct?

A final question on this: if I was to go on from here to find the natural frequencies/ etc., I would presume that it is okay to leave the matrices in their current form? I only ask that as the few examples I have seen in lectures only have 'M' matrices which are diagonal, but I presume that is reflective of the respective situation rather than a mathematical reason?

Thanks in advance for the help.

 

[KataKoniK]

Hi there,

I would approach this problem by first understanding the physical system and its components. In this case, we have a bar with two masses attached to it, and we want to derive the equations of motion for the system.

One approach that can be used to solve these types of problems is the Lagrangian method. This method involves defining a Lagrangian function, which is the difference between the kinetic and potential energies of the system. From this Lagrangian function, we can derive the equations of motion using the Euler-Lagrange equations.

In this case, the Lagrangian function would be:
L = T - U = \frac{1}{2}m(\dot{x_1}^2 + \dot{x_2}^2) + \frac{1}{2}k(x_1^2 + x_2^2) - mgh

Where T is the kinetic energy, U is the potential energy, m is the mass, k is the spring constant, and h is the height of the bar.

Using the Euler-Lagrange equations, we can obtain the following equations of motion:
m\ddot{x_1} + kx_1 = 0
2m\ddot{x_2} + kx_2 = 0

These equations are similar to the ones you have derived, but they take into account the masses and their positions on the bar. As for finding the natural frequencies, you can use these equations to obtain the characteristic equation and solve for the natural frequencies.

As for your method, it seems to be correct, but I would recommend using the Lagrangian method as it is a more generalized approach and can be applied to various systems. Also, as you mentioned, the diagonal matrices in lectures are reflective of the specific situation, but in this case, we have a 2-DOF system, so the matrices will not be diagonal.

Hope this helps! Let me know if you have any other questions.