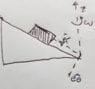
Like Tony Stark
- 182
- 6
- Homework Statement
- The wedge spins with angular velocity ##\omega##. There's a block of mass ##m## on it which is restricted by a slot to slide down. Determine the acceleration of the block. Is there any force acting on the walls of the slot? How can you calculate it?
- Relevant Equations
- ##\Sigma F_{e\theta}=m(2\dot r \dot {\theta})##
##\Sigma F_{er}=m(\ddot r -r\dot \theta^2)##
I think that the only force acting on the wall is the normal force caused by Coriolis force, so it can be calculated this way:
##N=m2\dot r \dot \theta##
But ##\dot r## is not constant, so how can I calculate it?
Then, I can't calculate the acceleration either since I don't have the value of ##\ddot r## to plug in the equation
##\Sigma F_{er}=m(\ddot r -r\dot \theta^2)##
##N=m2\dot r \dot \theta##
But ##\dot r## is not constant, so how can I calculate it?
Then, I can't calculate the acceleration either since I don't have the value of ##\ddot r## to plug in the equation
##\Sigma F_{er}=m(\ddot r -r\dot \theta^2)##