jcdenton
Hi !
I've been working on the following problem for quite some time now and I just can't figure out how to do it:
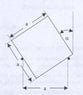
A homogeneous dice, whose edges have a length of a, is situated on two horizontal, thin, rigid rods. The rods are parallel to each other and are installed on the same height above the ground. Each of the rods is also parallel to one side of the dice. The coefficient of friction, μ, equals 0.2. For which angles α is the dice in a state of equilibrium ?
It is clear that the dice is in such a state for an angle α of 45°. However, due to friction, there must be additional angles, which are slightly bigger and smaller than 45°. But I do not know how to find these angles. I have tried to draw a diagram of all the forces involved in the problem, but I don't know which torques I need to consider and at which points I need to draw them.
It would be very nice if someone could help me solve this problem.
Thank you very much
Sebastian
I've been working on the following problem for quite some time now and I just can't figure out how to do it:
A homogeneous dice, whose edges have a length of a, is situated on two horizontal, thin, rigid rods. The rods are parallel to each other and are installed on the same height above the ground. Each of the rods is also parallel to one side of the dice. The coefficient of friction, μ, equals 0.2. For which angles α is the dice in a state of equilibrium ?
It is clear that the dice is in such a state for an angle α of 45°. However, due to friction, there must be additional angles, which are slightly bigger and smaller than 45°. But I do not know how to find these angles. I have tried to draw a diagram of all the forces involved in the problem, but I don't know which torques I need to consider and at which points I need to draw them.
It would be very nice if someone could help me solve this problem.
Thank you very much
Sebastian