Equivalent resistance/ geometric resistor network

[Goddar]

Homework Statement

hi guys,
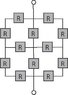
i'm having trouble applying Kirchhoff's laws to determine the equivalent resistance of this symmetrical array of resistors (see attachment); i think there is a quick trick, using 4 current loops, but i can't remember it... nor find relevant documentation
– this is not homework, I'm practicing for a test and never took this class... A shame, since i already graduated!–

Homework Equations

Kirchhoff's laws.

The Attempt at a Solution

Totally intuitive: R.

 

[Redbelly98]

The Attempt at a Solution

Totally intuitive: R.

Was that intuitive, or a total guess?

Here's a hint: imagine a voltage V is applied across the terminals.

What is the voltage at the very center of the grid?

What are the voltages at 1 grid-length to the left or right of the very center?

From those voltages, you can figure out the currents through the different resistors. What do you get for the total current in the circuit?

 

[Goddar]

you're right, i meant absolute guess...

so, i might be totally wrong here, because I'm very new to electrical circuits and still don't quite get a sense of it (to my greatest shame):
- do you mean that, given the symmetry of the arrangement, the center ought to be at potential V?
- by the same token, would the central side nodes be also at V?

But given that (and my attempts to apply Kirchhoff's the academic way), it would seem that no current flows through the central, horizontal branch, which would make the whole thing equivalent to 3 branches in parallel and, indeed, bring the overall resistance to R... which now, doesn't seem so intuitive because of this inert middle branch.

 

[willem2]

you're right, i meant absolute guess...

so, i might be totally wrong here, because I'm very new to electrical circuits and still don't quite get a sense of it (to my greatest shame):
- do you mean that, given the symmetry of the arrangement, the center ought to be at potential V?

No. Because of the vertical symmetry, the currents in the resistances below the
centerline are equal to the currents of the corresponding currents above it. The voltage
drops across those resistances are also equal.
consider the voltage drop across the 2 resistances above and below the centerpoint. the upper terminal is at V, and the bottom one at zero. What's the potential of the centerpoint?

Same story with the points left and right of the centerpoint.

 

[Goddar]

Right.. so, for the center points that would make it V/2 then?
but then there's still no potential difference through the horizontal middle branch and therefore no current... what i don't get is: the vertical symmetry is obvious (right = left), but the horizontal much less to me since current flows in 1 way and there could be a little drift across these middle branches, one way or the other.
i tried the long way, by assigning currents, determining voltage drops etc, and again the equations don't make sense unless this middle pass is idle... (but again, as you realize, i suck at circuits... so far)

 

[willem2]

you don't need the horizontal symmetry because of the vertical symmetry the center point and the point to the right and the left will all be at the same voltage, so it doesn't matter at all if there is a wire, a resistance or nothing at all between those points. you can simply remove them from the network, and it won't change the currents in any of the remaining resistances. and then all the rest of the netwerk can be reduced by combining series and parallel resistances.

There's horizontal symmetry too, but it's not as helpful.

If you really want to do it the hard way, IMO the most painless way of doing it is:

1. Combine any series or parallel resistances

2. Assign an unknown Voltage to all the points in the network, not connected to the power supply.

3. Now you can compute all the currents through the resistances as a function of the unknown voltages and the supply voltage.

4. Then use Kirchhoffs current law to give you one equation for each of the points
from step 1.

5. Solve the equations.

This will give you the minimum amount of equations, since there are always more resistances than network points

Of course once you have this:
2R(v-v1) + R(v2-v1) = 2Rv1
R(v-v2) + R(v1-v2) + R(v3-v2) = Rv2
2R(v-v3) + R(v2-v3) = 2Rv3

It will be much harder to spot any symmetry, so look for that first.

you'll probably get only 1 problem that needs this, with 5 resistors and 2 unknown
voltages.

 

[Goddar]

so the symmetry makes it all equivalent to 2 parallel-resistors-cluster, in series? and brings the overall resistance to R...
the symmetry argument still needs to sit in, i find it much easier to grasp in a cubic or spherical network, for some reason; if i imagine water flow instead of electrical here, i still get a sense that something might be going on in the middle, breaking horizontal symmetry but keeping vertical one..
Anyway, thanks for the help!

 

[vk6kro]

These puzzles pop up from time to time and one way to get them out is to join all points that have the same potential with pieces of wire. There should be no current flowing in these wires since they join points of equal voltage.

In this case, you can then also remove some components that are shorted out.

This turns a nasty exercise of solving 15 simultaneous equations into a mental arithmetic one, or at worst a calculator one.

You can tell it isn't a joke any more when the resistors all have oddball different values.