PhysicsMan999
- 32
- 0
Homework Statement
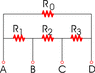
In the circuit shown, R1 = 0.810 Ω, R2 = 8.10 Ω, R3 = 81.0 Ω, and R0 = 810 Ω.
See attachment
Calculate the equivalent resistance of the circuit when a 7.70 V power supply is connected between points A and C.
Calculate the current through R0 and R1
Homework Equations
Series: resistances sum
Parallel: 1/Req=1/R1+1/R2...
The Attempt at a Solution
Okay so I'm not really understanding circuits well. From what I would gather R3 and R0 would be in series, but I'm just really confused about R1 and R2. And I'm not even 100% sure if R3 and R0 are actually in series since it branches off to D between them as well..