Piyu
- 45
- 0
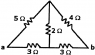
1. find the equivalent resistance across points a and b
I've used kirchhoff junction and loop rule to get a whole chunk of simultaneous equations but i can't seem to lay the finisher.
Assigning I_1 to I_4 in the clock wise manner starting from the 5 ohms resistor, and I_5 to the middle 2 ohms resistor. V = potential difference between a and b.
V=5I5+4I2=3I4+3I5
I=I1+I4=I2+I5
Ill end up with R=V/I = 15V/(8V-15I5-12I2. and here I am pretty much stuck with no way to change the remaining 2 to equations of V
The Attempt at a Solution
I've used kirchhoff junction and loop rule to get a whole chunk of simultaneous equations but i can't seem to lay the finisher.
Assigning I_1 to I_4 in the clock wise manner starting from the 5 ohms resistor, and I_5 to the middle 2 ohms resistor. V = potential difference between a and b.
V=5I5+4I2=3I4+3I5
I=I1+I4=I2+I5
Ill end up with R=V/I = 15V/(8V-15I5-12I2. and here I am pretty much stuck with no way to change the remaining 2 to equations of V