Estimating damping factor for steel in flexural oscillation

[Engineer_Phil]

I am trying to estimate the damping ratio of steel in bending. I have a situation where I need to know the dynamic response of an inverted pendulum. A picture is worth a thousand words, so here you go:

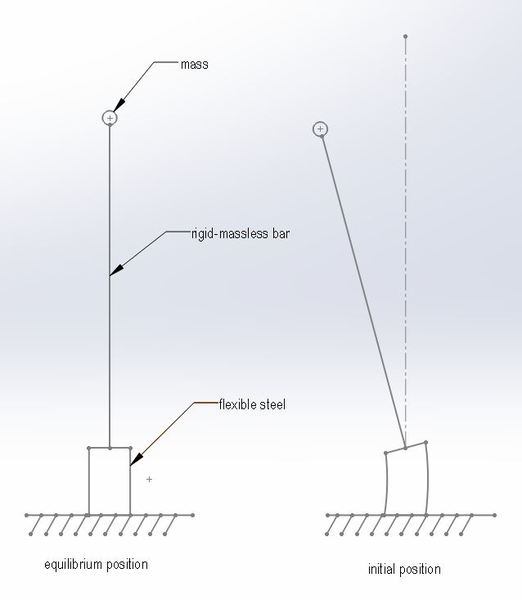
The vibration will be free; it is caused be the initial position of the system. I can calculate the stiffness of the flexural steel based on the length, cross section, and material properties.

The problem is estimating the damping. I want to know how long it takes the ocsillations to die down to a specified level.

I have done some research on google and so far I have only been able to find lengthy thesis full of differential equations and no real applicable conclusions. I am aware of the logarithmic decrement method, but I do not have the luxury of setting up a full scale model.

What I am looking for is some sort of relation between the geometry and the material properties to estimate the damping. Can someone point me in the right direction?

Thank you!

 

[AlephZero]

The amount of energy damped by the material in the steel plate itself will be very small. The main source of damping is likely to be the way the plate is fixed to the "rigid" base, and that usually defies any analysis. For example if it is clamped or bolted, tiny amounts of oil and grease in the joint can increase the damping by a surprisingly large amount (factors of 10 or more!)

The next biggest damping effect would probably be air resistance which is also hard to calculate.

If you want to do calculations with an "accurate" damping level, the best option is measure it. A reasonable ballpark figure would be about 1% or 2% of critical damping (and of that, maybe 0.1% is from the hysteresis of the steel plate as it bends, the rest is from other sources).

 

[Engineer_Phil]

The 'fixed' end condition is based upon the flexible steel plate being welded to a massive chunck of steel. But what I called the 'rigid massless bar' is bolted to the steel plate.

1% to 2% critical damping means there will be a lot of oscillations which is not what I am looking for. What would be a good way to increase the damping?

Just to satisfy my curiousity, how would you calculate the damping effect of the steel plate?

 

[AlephZero]

Lots of things you could think about doing:

• Bolting the "rigid bar" to the plate with some rubber washers (or a more specialized elastomer damping material) would be a start.
• Change the material of the steel plate to something like rubber.
• Replace the plate by a set of laminations that have to slide over each other with friction between them when it bends (like an old-style leaf spring).
• You can get self-adhesive sheets of damping material to apply to the surface of components that bend (like your plate) - though you might have a problem buying only a small quantity
• Add something to the structure to increase the air resistance (e.g. fix a flat plate to the rod)
• Or even immerse the whole device in a high viscosity liquid instead of air.

In real life (at least in my experience) the damping factors used in calculations are mostly based on experience and measurements of similar systems, not calculated from first principles.

 

[Engineer_Phil]

In real life (at least in my experience) the damping factors used in calculations are mostly based on experience and measurements of similar systems, not calculated from first principles.

Thanks for the help. Unfortunately this is a rare situation at our company and no one really has any experience estimating damping factors.

I find it hard to believe that everyone builds prototypes to test what their damping is, or make guesses based on prior projects. It seems like there would be a method of sometype out there to atleast get a close estimate. But maybe there are just too many factors to account for.

 

[timthereaper]

You can use a modified form of the formulas presented in the screenshots. The tables come from the textbook System Dynamics by Palm. You can set up an ODE of the form $m\ddot{x}+c\dot{x}+kx = 0$ and specify the way you want your x(t) to act and solve for your damping constant c. You'll probably have to use a modified form for the mass of your cantilevered beam because it assumes the beam's mass is distributed across the whole length up to the concentrated mass.

Hope that helps!

 

[Engineer_Phil]

I know how to evaluate what I want c or ζ to be. The problem is designing the system to give me that value.

 

[timthereaper]

So how is your system different than the cantilevered spring with a damping coefficient? I thought that you could build the ODE and solve. Is there something I've missed?