Estimating electric field strength

[Linus Pauling]

1. Estimate the electric field (strength and direction) at the point A.

5cmx5cm gridL

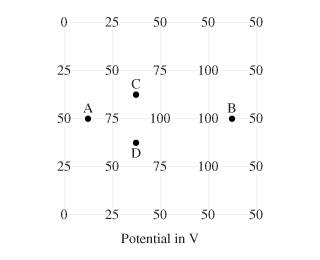
2. E = -dV/ds



3. I had four options, each a combination of 500 or 1000V/m for the E field strength and then left or right for the direction. I knew it must be to the left because the field points in the direction of decreasing potential, but how was the strength obtained (the answer is 500V/m)?

I did E = dV/ds = 12.5V/.00625m = 2000V/m, because point A is 1/8(5cm) from the left side of the grid...

 

[member 553083]

and then I divided by 4 because there are 4 boxes (1/2 of 5cm) between the left side and point A. So 2000V/m/4 = 500V/m.