Euclidian geometry: Construct circle trough point on angle bisector where

[Berrius]

Homework Statement

This is part from a larger construction, but I realized if i can construct this, i can do the larger construction. All ofcourse with ruler and compass.
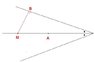
I have been given an angle with its bisector and a point on that bisector. I have to construct a circle trough that point (A), such that the lines from the angle are tangent lines to the circle.

The Attempt at a Solution

I have to find a point M and B such that AM = BM, and than i can construct the circle. But i have no idea how to do this.

 

[NascentOxygen]

Let's label the vertex to the right, O.
Construct a perpendicular at A, and extend it out to meet BO at T.
We have located two tangents to the circle, one being BO and the second being TA. These tangents together form angle BTA.

Hint: this angle forms a sort-of-hat which symmetrically sits atop the desired circle.