You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Euler Formula: Understanding (4.25) to (4.26)
- Thread starter pinkcashmere
- Start date
-
- Tags
- Euler Euler formula Formula Sine
AI Thread Summary
The discussion focuses on the transition from the expression ae^{jwt} + be^{-jwt} to Asin(wt + θ) using Euler's formulas and trigonometric identities. Participants express difficulty in identifying exponents from the uploaded material and inquire about the testing of the upload. Clarification is sought on the application of Euler's formula in this context. Ultimately, one participant confirms their understanding of the conversion process. The conversation highlights the importance of clear notation and effective use of mathematical identities.
Mathematics news on Phys.org
- 20,699
- 28,074
Although I downloaded and zoomed it I couldn't clearly identify the exponents. Did you test your upload?
jedishrfu
Mentor
- 15,511
- 10,243
Have you tried using the Euler formula:
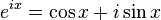 and some trig identities?
and some trig identities?
https://en.wikipedia.org/wiki/Euler's_formula
https://en.wikipedia.org/wiki/Euler's_formula
pinkcashmere
- 17
- 0
Basically, I want to know how you go fromfresh_42 said:Although I downloaded and zoomed it I couldn't clearly identify the exponents. Did you test your upload?
## ae^{jwt}## + ## be^{-jwt}##
to
##Asin(wt + \theta)##
pinkcashmere
- 17
- 0
ok, i got it now.
thanks
thanks
Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
Is it possible to arrange six pencils such that each one touches the other five? If so, how? This is an adaption of a Martin Gardner puzzle only I changed it from cigarettes to pencils and left out the clues because PF folks don’t need clues. From the book “My Best Mathematical and Logic Puzzles”. Dover, 1994.
I posted this in the Lame Math thread, but it's got me thinking.
Is there any validity to this? Or is it really just a mathematical trick?
Naively, I see that i2 + plus 12 does equal zero2.
But does this have a meaning?
I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero?
Ibix offered a rendering of the diagram using what I assume is matrix* notation...
Similar threads
- Replies
- 3
- Views
- 1K
- Replies
- 5
- Views
- 3K
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 10
- Views
- 3K
- Replies
- 6
- Views
- 2K
- Replies
- 40
- Views
- 7K
- Replies
- 0
- Views
- 1K
- Replies
- 38
- Views
- 11K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
-
I Geometry problem of interest with a 3-4-5 triangle
- Started by Charles Link
- Replies: 59
- General Math
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
