- #1
stunner5000pt
- 1,461
- 2
Evaluate the integral over the bounded closed region B
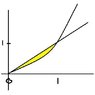
[tex] \int \int_{B} x^2 y^3 dx dy [/tex] B is the region bounded by y=x^2 and y =x
certainly the x=0 to x=1 will be the limits for the x part
but what about the y does it go from root y to y?
please help! i neeed to understand how to setup these little buggers
[tex] \int \int_{B} x^2 y^3 dx dy [/tex] B is the region bounded by y=x^2 and y =x
certainly the x=0 to x=1 will be the limits for the x part
but what about the y does it go from root y to y?
please help! i neeed to understand how to setup these little buggers