Expressing A Vector Given Another Vectors

[wiraimperia]

Homework Statement

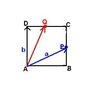
ABCD is a square (AB = AD = BC = CD). The point P and Q are located in the middle of BC and CD. If AP and AD is expressed by the name vector a and b, then AQ = ...
A) (1/2)a + (3/4)b
B) (1/3)a + (2/3)b
C) (3/4)a + (1/2)b
D) (2/3)a + (1/3)b
E) (2/3)a + (3/4)b

Homework Equations

Vector addition law (still confused)

The Attempt at a Solution

This problem comes in a competition about 4 months ago. I just chose the answer A (random guessing) and thank God the answer is A. But how do we find it?

 

[tiny-tim]

welcome to pf!

hi wiraimperia! welcome to pf!

for some reason, AD is called "b"

so let's call AB "d" …

then express everything in terms of b and d …

what do you get? ​

 

[ehild]

A picture always helps.

ehild

 

[tiny-tim]

 

[wiraimperia]

hi wiraimperia! welcome to pf!

for some reason, AD is called "b"

so let's call AB "d" …

then express everything in terms of b and d …

what do you get? ​

We refer to the multiple choice answers... Not a made-up answer... And I'm still confused why it is (1/2)a + (3/4)b

 

[ehild]

Pretend that it is a "made-up" problem and find the vector AQ in terms of a and b. Follow tiny-tim's hint.

ehild

 

[azizlwl]

Remember a vector can be represented by a segment of a line
You can put anywhere the line/vector with the same direction/parallel.

 

[Super Kirei]

Just draw two lines through Q, one parallel to b and the other parallel to a. These lines will cut b and a to the appropriate lengths and these lenghts can be determined by using the similarity triangles in the case of a and the 30-60 triangle in the case of b.