Expressing the Area of a Triangle in Surd Form

[odolwa99]

Homework Statement

Having a bit of trouble with this one, specifically the answer of (ii) (Q. diagram included as attachment). Can anyone help?

Many thanks.

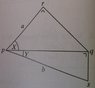
Q. In the given diagram, the angles prq & pqs are both right angles. The \anglerpq = X, \angleqps = Y, |pr| = a & |ps| = b. (i) By considering the triangles prq & psq, show that b = \frac{a}{cosXcosY}, (ii) If X = 45^o & Y = 30^o, express the area of \trianglepqs in terms of a. Give your answer in surd form

The Attempt at a Solution

Attempt: (i): cos = \frac{adjacent}{hypotenuse}
Thus, cosX = \frac{a}{|pq|} & cosY = \frac{|pq|}{b}
Therefore, cosX\cdotcosY = \frac{a}{|pq|}\cdot\frac{|pq|}{b} = \frac{a}{b}
And so, cosX\cdotcosY = \frac{a}{b} => b = \frac{a}{cosX\cdot cosY}

(ii) Area of triangle: \frac{1}{2}b\cdot|pq|\cdot sin30^o
1st, note that: cos45^o = \frac{1}{\sqrt{2}} & cos30^o = \frac{\sqrt{3}}{2}
Thus, b = \frac{a}{cosX\cdot cosY} => \frac{a}<br /> {1/\sqrt{2}\cdot\sqrt{3}/2} => \frac{a}{\sqrt{3}/2\sqrt{2}} => \frac{2\sqrt{2}a}{\sqrt{3}}
2nd, note that: cosX = \frac{a}{|pq|} => |pq| = \frac{a}{cos45^o} => |pq| = \frac{a}{1/\sqrt{2}} => |pq| = \sqrt{2}a
Now, \frac{1}{2}b\cdot|pq|\cdot sin30^o = \frac{1}{2}\cdot\frac{2\sqrt{2}a}{\sqrt{3}}\cdot \sqrt{2}a\cdot\frac{1}{2} => \frac{(2\sqrt{2}a)(\sqrt{2}a)}{4\sqrt{3}} => \frac{(\sqrt{2}a)(\sqrt{2}a)}{2\sqrt{3}} => \frac{2a^2}{2\sqrt{3}} => \frac{a^2}{\sqrt{3}}

Ans.: (From textbook): \frac{a^2\sqrt{3}}{3}

 

[LCKurtz]

I didn't check your steps, but look what happens if you rationalize the denominator in your answer.

 

[odolwa99]

Great. Thank you very much.

 

[Mark44]

Minor point: You are using => incorrectly in some (not all) places. For example, in the line that starts "Thus, b..." All of the => implications in that line should be =. Likewise in the last line.

Use = between two expressions that have the same value. Use => between two statements for which the first statement implies the second, such as 2x + 1 = 3 => x = 1.