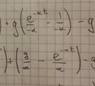Expressing y(t) including the effects of air resistance & gravity

[Cooojan]

Homework Statement

[/B]
Hi everyone! So I've got this similar problem as I posted yesterday, but this one
is slightly different due to the presence of gravity:

A particle in gravitational field $~~g$
starts traveling upward (positive direction) along the y-axis from $~~y=0$
with the initial speed $~~v_0≠0~~$,
where it faces air resistance $~~F_R$

$F_R = -mbv~~~~$ (where $~v~$ is the speed of the particle)

I have to show that the position of particle at any time can be expressed as following:

$y(t)= \frac 1b (v_0+ \frac gb)(1-e^{-bt})- \frac gb t$

Homework Equations

$\frac{dv}{dt}+bv = -g$

The Attempt at a Solution

[/B]
So I found out that the expression for speed of the particle in this case is:

$v(y) = \frac 1b(b(v_0)e^{-bt}+ge^{-bt}-g))~~~~$ (I believe this should be correct)

Further:

$v=\frac{dy}{dt} ~~~~⇒~~~~dy=v~dt~~~~⇒~~~~ \int \,dy= \int_0^t v\,dt ~~~~$ (unsure if I've taken limits correctly)

When I do this integration, what I get - is something that somehow reminds of solution,
which I was suppose to come to:

Iget:

$y(t)= \frac1b(v_0)(1-e^{-bt}) + g- e^{-bt} - \frac gbt$

when I should get:

$y(t)= \frac1b(v_0+ \frac gb )(1-e^{-bt}) - \frac gbt$

If someone could point out what exactly am I doing wrong, would be awesome!
Also if you can comment on if I'm taking limits correctly.
In this case it doesn't really metter, I guess, but generally speaking - should I take same integration limits on both sides or not?
(as with: $~~ \int \,dy= \int_0^t v\,dt ~~$)$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~Thanx~a~lot ! ~~$

 

[berkeman]

FR=−mbv F_R = -mbv~~~~ (where v ~v~ is the speed of the particle)

Just to clarify, you are given that the retarding force due to air resistance is proportional to the object's mass? That doesn't seem correct...

 

[Cooojan]

No no! Its proportional to particles speed. Acceleration would then be equal to "-bv"
As you can see further below - mass is not mentioned anywhere else in equations

 

[willem2]

You made a mistake when integrating. The integral of e^at is very easy to get wrong by mistake. I also think you dropped a g somewhere.
You can also look at the units too see which terms are wrong. y(t) = g + ... can't be right.

 

[Cooojan]

 

[Cooojan]

! Oh !
I forgot to mention that originaly, this was a 2D problem, so that is why I'm using $v_0~sinθ$ in my calculations on paper,
and not just $v_0$, as I did in my post.
But I already solved for x-axis, so I didnt want u guys to think of any unnecessities, while helping me out.
So I just turned the whole thing into a 1d problem. I hope u don't mind. :)
And also I used $b$ instead of $α$, just so it would be faster for me to write it down in $LaTeX$.

So that's what I did to get there...
I still can't get this right. If u have any suggestions, u r more then welcome to share))
Many thanx!

 

[willem2]

So that's what I did to get there...
I still can't get this right. If u have any suggestions, u r more then welcome to share))
Many thanx!

You're nearly there. The 1/a factors are ok now, but you forgot to multiply both terms with g here.

 

[Cooojan]

You're nearly there. The 1/a factors are ok now, but you forgot to multiply both terms with g here.

View attachment 213529

True story, my fault! Thank u)) How didnt I see this??
Was pretty close and even checked thrue integration several times... Now I got it right! Cant thank you enough))))))))))