- #1
assaftolko
- 171
- 0
Homework Statement
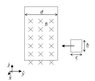
A rectangular loop moves with constant speed v towards an area in space with constant magnetic field B (As shown in the attachment). The loop enters this area and leaves it from the other side. Also given: d>c. Assume that t=0 when the left edge of the loop is just on the right edge of the magnetic field area. Assume positive induced emf when it generates induced current clock-wise in the loop.
Homework Equations
Well I'm asked to calculate 4 things in this problem, I'm interested in one of them:
Now, instead of moving with constant speed v, the loop is accelerated with constant acceleration a. The loop starts at rest when its left edge is just on the right edge of the magnetic field area. When will the induced current in the loop will be maximal?
The Attempt at a Solution
According to the solution the induced current will be maximal in two moments (and equal in both of them): When the loop is just about to completely enter the area of magnetic field and when the loop is just about to completely leave this area. Two questions:
1. As the loop leaves the area - its area that's subjected to the magnetic field decreases with time - so wouldn't we expect that the induced current will be maximal just as it starts to leave the area?
2. Why would the maximal induced current be the same in these 2 cases? Time is increasing as the problem starts - and since the induced emf is a function of t in the case of acceleration - how does it make sense that the induced emf will be equal like the solution states?