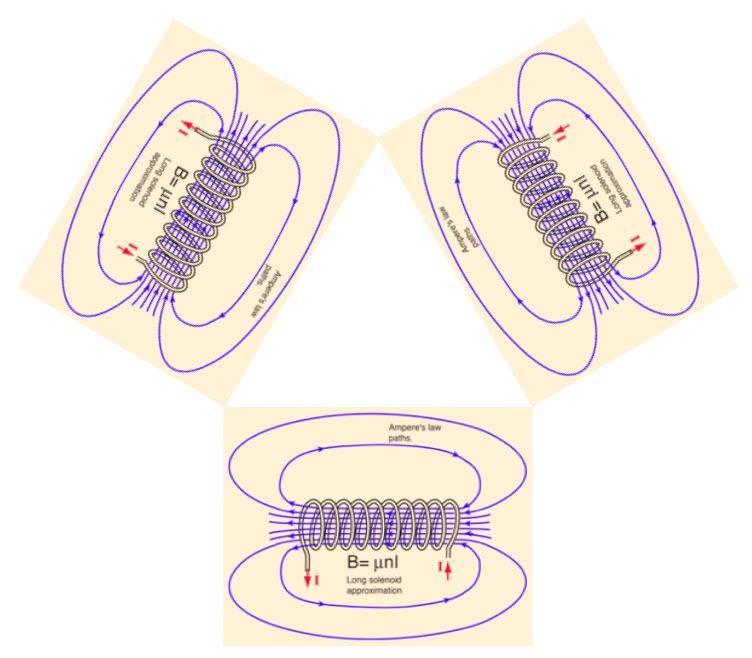
You know that for an infinite solenoid of radius ##R## the field is zero at distance ##r>R## from the axis. No solenoid is infinite, so at ##r>R## the magnetic field is approximately zero. The approximation becomes better and the field is closer to zero the closer you come to the solenoid. This is shown graphically in the pictures you scared up. Point Y is farthest from all solenoids therefore you are supposed to conclude that the field is strongest there, when you add the fields as vectors, where the infinite solenoid approximation is worst.
Having said that, let's see what Maxwell's equations have to say about this. One of these equations says that magnetic field lines form closed loops. Another one, a.k.a. Ampere's law says that if you take a line integral around a closed loop, the result is proportional to the current enclosed by the loop. So let's draw an arrow representing the magnetic field at point Y. It's part of a closed loop. Let's draw it as a closed oriented magnetic field line loop entirely inside the triangle. The integral ##\oint \vec B \cdot d\vec l## cannot be zero because the magnetic field is always along the contour, yet there is no current cutting through the plane of the loop. This is a contradiction. My initial thought when I saw this was that the field inside the triangle is zero.Please be more patient. It's Sunday after all.