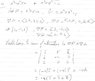s3a
- 814
- 8
I have attached both the question and the solution.
I just have questions as to why the solution is the way it is (sorry if they seem stupid but, while I get how to do it mechanically, I don't understand the fundamental reasoning as to why anything is being done):
1) Why are we taking the gradients?
2) Why are we then taking the cross product of the two gradients?
My attempt to answer these questions (I'd still appreciate confirmation for stuff that I am right about):
Gradients at a point in 3D spaces are analogous to derivatives at a point in 2D spaces but taking the gradient of a curve in 3D space yields a normal vector to a point on the curve instead of a line tangent to the curve in the 2D space scenario. I'm guessing these two gradient vectors are supposed to be perpendicular and that finding their cross product would yield a tangent vector to the intersection of the two curves but I don't get why this is so.
Any input would be GREATLY appreciated!
Thanks in advance!
I just have questions as to why the solution is the way it is (sorry if they seem stupid but, while I get how to do it mechanically, I don't understand the fundamental reasoning as to why anything is being done):
1) Why are we taking the gradients?
2) Why are we then taking the cross product of the two gradients?
My attempt to answer these questions (I'd still appreciate confirmation for stuff that I am right about):
Gradients at a point in 3D spaces are analogous to derivatives at a point in 2D spaces but taking the gradient of a curve in 3D space yields a normal vector to a point on the curve instead of a line tangent to the curve in the 2D space scenario. I'm guessing these two gradient vectors are supposed to be perpendicular and that finding their cross product would yield a tangent vector to the intersection of the two curves but I don't get why this is so.
Any input would be GREATLY appreciated!
Thanks in advance!
Attachments
Last edited: