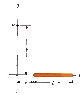Keithkent09
- 33
- 0
The thin, uniformly charged rod shown in the figure below has a linear charge density λ. Find an expression for the electric potential at P. (Use k_e for ke, lambda for λ, a, b, and L as necessary.)
dV=k*dq/r
lambda*dx=dq
I integrated using the above equations and went from 0 to L. I thought this was the right way to do it but I keep getting the wrong answer.
Homework Equations
dV=k*dq/r
lambda*dx=dq
The Attempt at a Solution
I integrated using the above equations and went from 0 to L. I thought this was the right way to do it but I keep getting the wrong answer.