xxlvh
- 9
- 0
1. The density of part A (p)(kg/m^3) and in part B (p/2)(kg/m^3). Find the coordinate (x,y) of the center of mass of this object.
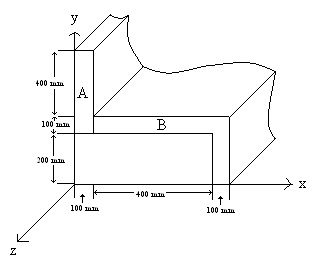
(consider a piece of the object that is one meter in the z direction)
2. R = sum(m*r) / sum(m)...maybe? I am completely stumped on how to start this problem my teacher has done no sample problems that are anything like this, not even anything in 3D, if anyone could at least provide a hint to get me started on this one? Would be greatly appreciated.
(consider a piece of the object that is one meter in the z direction)
2. R = sum(m*r) / sum(m)...maybe? I am completely stumped on how to start this problem my teacher has done no sample problems that are anything like this, not even anything in 3D, if anyone could at least provide a hint to get me started on this one? Would be greatly appreciated.
Last edited: