hogrampage
- 107
- 1
Homework Statement
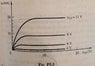
A MOSFET has the set of v-I characteristics shown in Fig. P5.5.
What are the values of K and VTR?
Homework Equations
iD=K(VGS-VTR)2
The Attempt at a Solution
I have looked in the book and all of the example problems give VTR, but it doesn't show how to actually get the K and VTR values based on the graph. I really have no idea what to do.
The answer in the book says K=0.25 mA/V2 and VTR=2V. Is VTR 2V because VGS increases by 2V?