snshusat161
- 213
- 1
Homework Statement
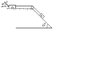
Two rectangular blocks of weight, A = 150 N and B = 100N are connected by a string and rest on an inclined plane and on a horizontal surface as shown in the figure. The coefficient of friction for all contiguous surfaces is \mu = 0.2. Find the magnitude and direction of the least force P at which the motion of the block will impend.
Homework Equations
frictional force = \mu. N
where N = normal rection
The Attempt at a Solution
I had calculated T In the string from box A and then I have made two equations from box B. The only think I am unable to find is the angle \theta. Somebody help me to find that angle.
Answer: P = 161.7 N and \theta = 11.31 degree
sorry for the poor diagram. I don't have a scanner.