Find masses on an equilibrium plane

[Naldo6]

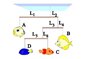
Can anyone help me on how to calculate mass C, mass D, and mass A from the diagram in the atachment whose is in equilibrium if:

The object B has mass of 0.785 kg. Determine the mass of object C. Assume L1 = 30.4 cm, L2 = 7.50 cm, L3 = 14.6 cm, L4 = 5.00 cm, L5 = 16.8 cm and L6 = 5.00 cm. (Neglect the weights of the crossbars.)

 

[heth]

Same as your previous questions - show some work and an attempt at a solution, as per the forum rules.

 

[thomate1]

To calculate the masses of objects C, D, and A on the equilibrium plane, we can use the principle of moments. This principle states that in a system at equilibrium, the sum of clockwise moments is equal to the sum of counterclockwise moments.

First, we can calculate the moment of object B by multiplying its mass (0.785 kg) by its distance from the equilibrium point, which is L2 + L3 = 7.50 cm + 14.6 cm = 22.1 cm.

Next, we can set up the equation for the principle of moments:

(clockwise moments) = (counterclockwise moments)

(0.785 kg)(22.1 cm) = (mass C)(L1) + (mass D)(L4) + (mass A)(L5)

Substituting in the given values for L1, L4, and L5, we get:

(0.785 kg)(22.1 cm) = (mass C)(30.4 cm) + (mass D)(5.00 cm) + (mass A)(16.8 cm)

To solve for the masses, we need to have three equations. We can use the fact that the total mass on the equilibrium plane is equal to the sum of the masses of objects B, C, D, and A:

mass B + mass C + mass D + mass A = total mass

Substituting in the given value for mass B (0.785 kg), we get:

0.785 kg + mass C + mass D + mass A = total mass

We can also use the fact that the total length of the equilibrium plane is equal to the sum of the lengths of the objects:

L1 + L2 + L3 + L4 + L5 + L6 = total length

Substituting in the given values for L1, L2, L3, L4, L5, and L6, we get:

30.4 cm + 7.50 cm + 14.6 cm + 5.00 cm + 16.8 cm + 5.00 cm = total length

Simplifying, we get:

79.3 cm = total length

Now, we have a system of three equations with three unknowns (mass C, mass D, and mass A). We can solve this system using algebraic methods, such as substitution or elimination, to find the masses