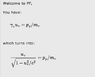Find Speed of Electron w/ Same Momentum as Proton at 0.62c

[j2dabizo]

Help solving the speed for and electron, having same momentum as a proton at 0.62c??

Homework Statement

A proton moves with a speed of 0.62c. Find the speed of an electron that has the same momentum. (Express the answer as the quantity of one minus a number times c.)

Homework Equations

p_p=p_e
or
y_pm_pu_p=y_em_eu_e

The Attempt at a Solution

Known:
m_p= 938.27 MeV/c²
u_p= 0.62c
m_e=0.511 MeV/c²

Solve for y_p= 1/sq rt 1-(0.62)²

y_p= 1.27453

so...

(1.27453)*(938.27MeV/c²)*(0.62c) = (0.511MeV/c²)*(y_e)*(u_e)

(741.429 MeV/c²*c) = (0.511MeV/c²)*(y_e)*(u_e)

1450.937c = (y_e)*(u_e)

Now this is where I get confused with the algebra...and need help getting thru it.

Please help! I've been struggling for 2 days on this and have finally broken down. I have one more oppurtunity to give the correct answer.

Thanks for the help..appreciate it.

 

[cepheid]

Welcome to PF,

You have:

\gamma_e u_e = p_p / m_e

which turns into:

\frac{u_e}{\sqrt{1-u_e^2/c^2}} = p_p /m_e

You need to solve for u_e. I would say that it would help to get rid of the square root by squaring both sides of the equation. It would also help to get rid of the fraction by multiplying both sides by the denominator of the left-hand side (after you've squared). Then you have some terms that contain u_e and some that don't. Collect all the terms that contain u_e in order to isolate it. EDIT: and to avoid clutter, don't plug in numbers until the very end.

 

[j2dabizo]

honestly, it's been a while since I took intro physics 1 and 2, about 10 years.

I'm stuck on getting u<sub>e isolated on the left side. Can you just run through the equation so I can see how its done?

I'm a fast learner..so once I see it done once, I remember, just been a long time since I've done this.</sub>

 

[j2dabizo]

anyone?

please help me solve this...i am truly stuck here

 

[cepheid]

honestly, it's been a while since I took intro physics 1 and 2, about 10 years.

Well, this is pure algebra at this point. There wasn't much actual physics in this problem, except for recognizing the equation for relativistic momentum, and equating the momenta of the two particles, since the problem stated that they were the same. How long ago was it since you took algebra?

I'm stuck on getting u_{e isolated on the left side. Can you just run through the equation so I can see how its done?}

<sub>Okay, we normally don't do people's homework for them, but since you've given it a solid attempt and shown your work, and indicated which parts you're having trouble with, I think the forum rules have been satisfied. By the way, did the LaTeX (fancy math) equations from my last post show up for you? I'm asking because physicsforums recently changed what software it uses to generate equations from LaTeX code, and it hasn't been working for some people. A screenshot of my previous post is attached just in case. Anyway, here are the algebraic steps that I would take:

We start with this:

\gamma_e u_e = p_p / m_e

and we know what gamma is:

\frac{u_e}{\sqrt{1-u_e^2/c^2}} = \frac{p_p}{m_e}

Now at this point, I would do exactly what I suggested to you before -- square both sides of the equation:

\frac{u^2_e}{1-u_e^2/c^2} = \left(\frac{p_p}{m_e}\right)^2

Next, I would multiply both sides of the equation by the denominator of the left-hand side (in order to get rid of the fraction):

u^2_e=(1-u_e^2/c^2)\left(\frac{p_p}{m_e}\right)^2

Now, expand the right hand side of the equation by multiplying (remember the distributive property of multiplication):

u^2_e = \left(\frac{p_p}{m_e}\right)^2 - \frac{u_e^2}{c^2}\left(\frac{p_p}{m_e}\right)^2

Now collect both terms that have a factor of u_e^2 on the left hand side:

u^2_e + \frac{u_e^2}{c^2}\left(\frac{p_p}{m_e}\right)^2 = \left(\frac{p_p}{m_e}\right)^2

Now, on the left hand side, there are two terms, both of which have a u_e^2 in them. As a result, you can factor out the u_e^2 in order to isolate it:

u^2_e\left[1 + \frac{(p_p /m_e)^2}{c^2}\right] = \left(\frac{p_p}{m_e}\right)^2

Now we can just divide both sides of the equation by everything that is in the square brackets, in order to leave the u_e^2 by itself on the left-hand side:

u^2_e = \frac{(p_p/m_e)^2}{1 + (p_p /m_e)^2/c^2}

To get ue, you just take the square root of both sides of the equation:

u_e = \frac{p_p/m_e}{[1 + (p_p /m_e)^2/c^2]^{1/2}}

NOW you can substitute in the expressions for pp, and then the numerical values. I didn't do this before, because I wanted to avoid clutter and make things easier to keep track of (as well as avoiding unnecessary calculator steps). So, keep things algebraic until the very end. The expression above becomes:

u_e = \frac{\gamma_p m_p u_p/m_e}{[1 + (\gamma_p m_p u_p /m_e)^2/c^2]^{1/2}}

Now everything is expressed in terms of known quantities, for which you can plug in the values. Let me know whether the equations in this post show up for you. If not, I can post a screenshot of it as well.</sub>

 

[j2dabizo]

Hi,
Yes the software did work and the equation do show up for me. It's been a while since algebra also, but I should know this, you are correct. Most times I just need to see a sample worked so I remember some of the rules/steps of algebra.

I'm taking modern physics online and there isn't much teaching...basically teach yourself. So seeing an equation really helps me and will be a guide for later problems.

I did give this my sincere attempt, thank you for your help and I'm sure you will be seeing me around here the next couple of months.

Appreciate it!