Fatima Hasan
- 315
- 14
- Homework Statement
- A 300 V DC separately excited motor has the parameters Ra= 0.409, C= 1.90986 V rad/s The motor drives a constant load torque of value 286.479 Nm at speed = 1200 rpm
Part 1: If the motor needs to be braked using dynamic braking and that is by using a braking resistance of value Rb=0.6
a) The braking torque at the instant of braking
b) The braking torque when the machine speed has decreased to 800 rpm
c) The braking torque when the machine speed becomes zero.
- Relevant Equations
- -
Here's my attempt for part 1a:
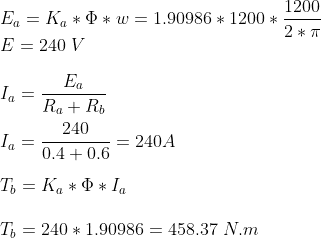
What I am not sure about is the direction, is it in the opposite direction (= - 458.37 N.m ) or it's positive?
Thanks,
What I am not sure about is the direction, is it in the opposite direction (= - 458.37 N.m ) or it's positive?
Thanks,