Find the charge on each capacitor

[Gonger]

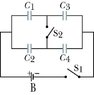
I'm trying to do this problem, its is posted below, where I have a circuit with four capacitors and I have to determine the charge on each one. I've been trying to follow an example from my textbook but that's not really helping me. I've been also trying to break it down with capacitors in parallel and in series, but I keep getting stuck. Anyone have any suggestions for any of this. There is a diagram of the circuit in the attachement. And this is the question:

In the figure, battery B supplies 18 V. Find the charge on each capacitor first when only switch S1 is closed. Take C1=1.3 µF, C2=2.3 µF, C3=3.6 µF, and C4=4.2 µF.

Thanks in advance.

 

[mewmew]

If s1 is closed the top and bottom two are in series and then you have two that are in parallel.

Edit: If s2 is closed first than you simply have the left set and right set in parallel and then the two equivelent are in series.

 

[Gonger]

yeah I've got that all figured out, its calculating it from there that I am having problems with.

 

[Corneo]

I would first calculate the effective capacitance of the circuit.

Since C1 and C3 are in series then their effective capacitance is C_{13} = \{ \frac {1}{C_1} + \frac {1}{C_3}\}^{-1}

Like wise the effective capacitor between C2 and C4 is C_{24} = \{ \frac {1}{C_2} + \frac {1}{C_4} \}^{-1}

Now you can use the definition of a capitance to find out the charge in C_{i}

Q = C_{i} V

Then you use the fact that capacitors in series have the same charge, Q. While capacitors in parallel have the same potential, V.