Find the conditions for the static coef. for non-slip conditions

[Hernaner28]

Homework Statement

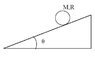
It's a cilinder of mass M and radius R rolling without slipping and I'm asked to find the maximum value of the static friction coefficient for the cilinder to roll without slipping.

Homework Equations

Non-slip conditions:
$$\displaystyle v=\omega R$$
$$\displaystyle a=\alpha R$$

Torque:
$$\displaystyle \tau =I\alpha$$

The Attempt at a Solution

Net force in axis X (my axis is along with the inclined plane):

$$\displaystyle -mg\sin \theta -{{\mu }_{s}}N=ma$$

Equation in axis y will give me the normal force:

$$\displaystyle N=mg\cos \theta$$
So:
$$\displaystyle -mg\sin \theta -{{\mu }_{s}}mg\cos \theta =ma$$
Solving for u:

$$\displaystyle {{\mu }_{s}}=\frac{-g\sin \theta -a}{g\cos \theta }=\frac{-g\sin \theta -\alpha R}{g\cos \theta }$$

So I need to find out the angular aceleration:

$$\displaystyle \tau =I\alpha$$
$$\displaystyle -{{\mu }_{s}}mg\cos \theta \cdot R=\frac{1}{2}m{{R}^{2}}\cdot \alpha$$
$$\displaystyle \alpha =\frac{-2g{{\mu }_{s}}\cos \theta }{R}$$

Replacing alpha in the equation I get that:
$$\displaystyle {{\mu }_{s}}\le \tan \theta$$

But the option marked as correct is:
$$\displaystyle {{\mu }_{s}}\ge \frac{\tan \theta }{3}$$

any help?

Thanks!

 

[azizlwl]

Check your I

 

[Hernaner28]

What's wrong out the inertia of the cilinder? Isn't it 1/2*MR^2? Thank you!

 

[Yukoel]

Hello Hernaner28,
You have implicitly assumed the limiting friction case in your rolling situation (fixing f_s=μN )
First of all treat friction as an unknown independent of the normal reaction of the cylinder on the inclined plane to get an expression for friction in terms of Mass of object,the inclination of the plane ,The radius and the Moment of inertia.Now the maximum friction that your incline can offer at the given N is ____________?(answer) So your calculated friction must not exceed _________?
Try to answer them and using the expression that comes as an interpretation calculate the condition again.I pretty much think this gives the actual answer as marked.Does this help?


regards
Yukoel

 

[Hernaner28]

But what was wrong about what I did? I worked with the limiting friction case because that would be the maximum coefficient of friction... that's why I finally get it has to be "less or equal".

Thanks!

 

[Yukoel]

But what was wrong about what I did? I worked with the limiting friction case because that would be the maximum coefficient of friction... that's why I finally get it has to be "less or equal".

Thanks!

Hello again!
Less than or equal to what?The maximum value isn't it?There should be a separate equation for the general expression of friction isn't it?Here is an advised algorithm .Find the general expression for friction for the non limiting case (i.e. not involving the usage of N ;just treat f as an unknown fully and just apply the pure rolling rolling condition with Gravity and friction ;get an expression and compare it with the maximum value of friction sought).Now let us see -What if the maximum value of friction is less than this required value of friction? There will be inevitable slipping right?
By the way the expression for friction that comes from the general case will give you the general expression for friction for a pure rolling body on an inclined plane.
Does this help?
regards
Yukoel

 

[Hernaner28]

Less or equal to tan(theta) as I finnaly worked out. I understand your thinking but I don't understand what is the difference between mine and yours, and what's the mistake about mine..

Thanks

 

[Yukoel]

Less or equal to tan(theta) as I finnaly worked out. I understand your thinking but I don't understand what is the difference between mine and yours, and what's the mistake about mine..

Thanks

Hello
I think you have by mistake yielded your derivations to a≥Rα.Contradictory to pure rolling isn't it?(The last step quoted)

regards
Yukoel

 

[Hernaner28]

Ah yes, you're right. So what is what I got? Because it is not incorrect but maybe it is not what I was asked

 

[azizlwl]

$$\displaystyle -mg\sin \theta -{{\mu }_{s}}N=ma$$

Equation in axis y will give me the normal force:

[

Thanks!

ma =mgsinθ-friction

 

[Hernaner28]

No, both forces point the same direction. The cilinder rolls downward so friction force does an opposite torque (downward).

But Yukoel, what was what I got then?

 

[azizlwl]

No, both forces point the same direction. The cilinder rolls downward so friction force does an opposite torque (downward).

But Yukoel, what was what I got then?

How the cyclinder roll counter clockwise?
Where the torque comes from?
The mgsinθ acts through the center of the cylinder.

 

[Hernaner28]

Ah yes you're right :D ! THANKS! Anyway, let's assume the last result is fine, then, what's the meaning of what I got? Is it the maximum coefficient of friction for the cilinder not to slip?

 

[Hernaner28]

I don't know why but now I get the correct answer... even with my first thinking (nothing was wrong about it). I think it was because of the direction of the force which azizlwl corrected.

THANKS!

 

[Hernaner28]

I get:

$$\displaystyle F=\frac{mg\sin \theta }{3}$$

The friction F force is:

$$\displaystyle {{\mu }_{s}}mg\cos \theta =\frac{mg\sin \theta }{3}$$

$$\displaystyle {{\mu }_{s}}=\frac{\tan \theta }{3}$$

For the limit case... so that would be the minimum value, or maximum?

 

[azizlwl]

The exact answer is μ≥ (2/7)tanθ
The maximum ratio friction/N is μ_s.

 

[Yukoel]

Ah yes, you're right. So what is what I got? Because it is not incorrect but maybe it is not what I was asked

Hmm... I am not so sure but it is a kind of slipping on the limiting case (as azizlwl points out there are sign mistakes in your equations).
Let me get to point on signs here
You can take friction arbitrarily let us suppose.For pure rolling the point of contact has to be at rest. Suppose the gravity and friction are in the same direction and look at the bottom .It will be accelerated.This is why friction has to be on the opposite of gravity.
This however has nothing to do with limiting cases.As a matter fact it is quite comfortable to take things down the incline as positive.
regards
Yukoel

 

[Hernaner28]

Yukoel, I got the correct answer now:

$$\displaystyle {{\mu }_{s}}=\frac{\tan \theta }{3}$$

But that is a equality, not inequality, now I have to decide the sign of the inequality. That value is the minimum or maximum value for the cilinder not to slip?

 

[Yukoel]

The exact answer is μ≥ (2/7)tanθ
The maximum ratio friction/N is μ_s.

Hello azizlwl
I think you have mistaken cylinder as a sphere (I=(2/5)M*(r^2)
However for cylinders (I=(1/2)M(r^2) )
I am pretty much sure that the answer sought as third of the value of tan(θ) is correct for the cylinder. And (5/2) times your answer your answer is correct for the sphere.

 

[azizlwl]

Hello azizlwl
I think you have mistaken cylinder as a sphere (I=(2/5)M*(r^2)
However for cylinders (I=(1/2)M(r^2) )
I am pretty much sure that the answer sought as third of the value of tan(θ) is correct for the cylinder. And (5/2) times your answer your answer is correct for the sphere.

Yes you are right, I made a mistake there. Thanks.

 

[Yukoel]

Yukoel, I got the correct answer now:

$$\displaystyle {{\mu }_{s}}=\frac{\tan \theta }{3}$$

But that is a equality, not inequality, now I have to decide the sign of the inequality. That value is the minimum or maximum value for the cilinder not to slip?

You had begun with the limiting case right? You had to have a limiting answer .Now think static friction had to atleast have this value of friction you derived .A little bit non mathematically this should be the least value.
Now calculate off the general value of friction for a body with a given I,M,θ(for incline)and R will you? This value of friction gives a general formula for f,and a(acceleration).You can use this for future reference too.
regards
Yukoel

 

[Hernaner28]

Alright then that's correct! Calculating for the general case I get that the friction force (not mu) should be:

$$\displaystyle F=\frac{IMg\sin \theta}{{{R}^{2}}+I}$$

Now how can I interpret this result?

 

[Yukoel]

Alright then that's correct! Calculating for the general case I get that the friction force (not mu) should be:

$$\displaystyle F=\frac{Img\sin \theta}{{{R}^{2}}+I}$$

Now how can I interpret this result?

$$\displaystyle F=\frac{Img\sin \theta}{{m{R}^{2}}+I}$$
Correct formula .
Now make it less than or equal to μmg cos(θ)- the maximum value of friction.And then substitute the value of I.
You will be done.
regards
Yukoel

 

[Hernaner28]

Alright but that general value of F indicates the unique value for an unique situation (given all that parameters) but that value has a upper bound which would be the maximum it may have not to slip (I am getting it! so, if I make it less than or equal to umgcos(theta) I am actually bounding the result to find the minimun coefficient, right?THANKSS!

 

[Yukoel]

Hello Harnaner28

Alright but that general value of F indicates the unique value for an unique situation (given all that parameters)

Not exactly to say .Your value for f works good for any given body with a given I ,M and R.Though to say it indicates rolling as a precondition.

but that value has a upper bound which would be the maximum it may have not to slip (I am getting it!

Yes this is true.

so, if I make it less than or equal to umgcos(theta) I am actually bounding the result to find the minimun coefficient, right?

Yes indeed .But it was not intended ,you bounded the friction force but mathematical rules yielded µ on the right side ,just to say.

Was this helpful?
regards
Yukoel