Dawg91
- 1
- 0
The circuit: http://www.webassign.net/walker/21-33alt.gif
The question reads:
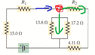
Consider the group of resistors in the figure below, where R1 = 14.1 Ω and R2 = 8.35 Ω. The current flowing through the 8.35-Ω resistor is 1.22 A. What is the voltage of the battery?
I found that the equivalent resistance was 15Ω + 14.1Ω + 4.74Ω = 33.84Ω,
and V=IR, so V = 33.84Ω x 1.22A = 41.3V.
I don't know where I'm going wrong.
The question reads:
Consider the group of resistors in the figure below, where R1 = 14.1 Ω and R2 = 8.35 Ω. The current flowing through the 8.35-Ω resistor is 1.22 A. What is the voltage of the battery?
I found that the equivalent resistance was 15Ω + 14.1Ω + 4.74Ω = 33.84Ω,
and V=IR, so V = 33.84Ω x 1.22A = 41.3V.
I don't know where I'm going wrong.