orthogonal
- 10
- 0
Hey all,
I am trying to find a function which will give me a family of curves similar to the one shown below. What I am hoping is that a single parameter will control whether the curve starts out slow (like the blue one) or whether the curve starts out fast (like the green one) or whether it is a linear ramp.
Does anyone know of a class of curves like this?
I can find plenty of curves which behave similar to the blue curve (ex. arctan, erf) but none like the green one.
Thanks,
Orthogonal
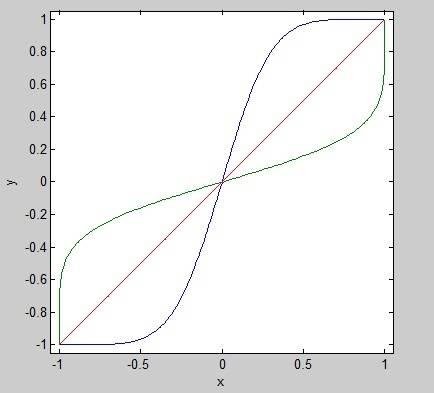
I am trying to find a function which will give me a family of curves similar to the one shown below. What I am hoping is that a single parameter will control whether the curve starts out slow (like the blue one) or whether the curve starts out fast (like the green one) or whether it is a linear ramp.
Does anyone know of a class of curves like this?
I can find plenty of curves which behave similar to the blue curve (ex. arctan, erf) but none like the green one.
Thanks,
Orthogonal
Last edited: