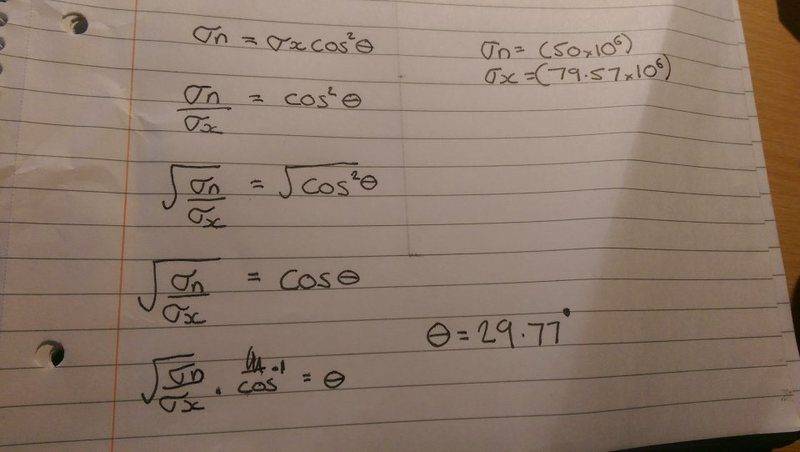Mechaman
- 37
- 1
Member warned about posting without the HW template
Not sure if I'm doing this right. I have an angle theta to find but the cosine has been squared. I brought over inverse cosine to multiply to leave theta on its own. I was told the answer should be closer to 37 degrees? Am I doing something wrong here?