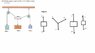Finding Angles 1 & 2 in Fig. 4-51

  • Thread starter Miike012
  • Start date
  • Tags
    Angle
In summary, finding angles 1 and 2 in Fig. 4-51 is important for determining measurements and relationships between lines and angles in a geometric figure. This can be done by using the properties and rules of geometry, as well as tools like a protractor and ruler. Labeling these angles is important for clear communication and there are many real-life applications, such as in construction and navigation.
  • #1
Miike012
1,009
0
Find the angles '1 and '2 in Fig. 4–51 if all the weights
are at rest.

Solution: The picture is on the paint document... I also drew some diagrams to help solve the problem.. I wanted to know if the diagrams were correct? Anyways as I proceed to solve for angle 1 and 2 it is hard because I don't know how to pull all the information together...
 

Attachments

  • Diagram.jpg
    Diagram.jpg
    12.3 KB · Views: 432
Physics news on Phys.org
  • #2
i think your diagrams are correct. Now system is at rest so all the forces acting in opposite directions are equal.
 

FAQ: Finding Angles 1 & 2 in Fig. 4-51

What is the significance of finding angles 1 and 2 in Fig. 4-51?

Finding angles 1 and 2 in Fig. 4-51 is important because it allows us to determine the exact measurements and relationships between different lines and angles in a geometric figure. This can help us solve problems and make accurate calculations.

How do you find angles 1 and 2 in Fig. 4-51?

To find angles 1 and 2 in Fig. 4-51, you can use the properties and rules of geometry, such as the sum of angles in a triangle and the properties of parallel lines. You may also need to use measurements of other angles or sides in the figure to solve for angles 1 and 2.

What tools or methods can be used to find angles 1 and 2 in Fig. 4-51?

Some tools that can be used to find angles 1 and 2 in Fig. 4-51 include a protractor, ruler, and compass. These tools can help you accurately measure and construct angles and lines in the figure. Additionally, algebraic methods and geometric formulas can also be used to find angles 1 and 2.

Why is it important to label angles 1 and 2 in Fig. 4-51?

Labeling angles 1 and 2 in Fig. 4-51 is important because it allows us to refer to them specifically when solving problems or communicating about the figure. This helps eliminate confusion and ensures that everyone is on the same page when discussing the angles.

What are some real-life applications of finding angles 1 and 2 in Fig. 4-51?

Finding angles 1 and 2 in Fig. 4-51 can be useful in various real-life situations, such as measuring and constructing buildings, designing structures and objects, and navigating using maps and compasses. It can also be helpful in fields such as engineering, architecture, and surveying.

Similar threads

Path on Cone Fig.1: Angle ACP is 90°?
Replies
28
Views
2K
A moving boat with a flag on its mast
Replies
15
Views
539
Refraction through different mediums: calculating multiple angles help
Replies
6
Views
1K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
501
For a Pendulum: Knowing Acceleration Find Maximum Angle
Replies
26
Views
2K
Calculate the best angle for maximum light dispersion through a medium
Replies
2
Views
1K
Finding the angle at the apex of a rhomb with incoming linear wave
Replies
12
Views
2K
The Relationship Between Masses and Angles in a Pulley System
Replies
29
Views
2K
2 unknown Forces+known resultant force
Replies
1
Views
2K
Calculating Unknown Forces in a Vector Diagram
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top