qweazy
- 13
- 0
Homework Statement
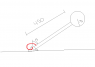
When Θ=0, the assembly is held at rest, and the torsional spring is untwisted. If the assembly is released and falls downward, determine its angular velocity at the instant Θ=90°. Rod AB has a mass of 6kg, and disk has a mass of 9kg.
Rod is 450mm and disk has a radius of 75mm
So there is a pin holding the assembly upwards which is when Θ=0 and at the pin there is a torsional spring with constant of k=20N m/rad. One end of the rod is attached to the pin and the other is attached to the disk.
Homework Equations
T1+∑U=T2
The Attempt at a Solution
So first I found the center of mass of the combined mass
I called mass of the rod M and mass of disk m.
Center of mass = (.5(.45)6+(.45+.075)9)/(6+9)= .405m
Then I found the moment of inertia
I=(1/3)(6(.45)^2)+(3/2)(9)(.075)^2+9(.525)^2= 2.96
T1=0 since the assembly started from rest.
Then I found T2
.5mv^2+.5Iω^2
.5(M+m)(.405ω)^2+.5(2.96)ω^2=2.71ω^2
Solved for the potential energy of the spring
.5(20)(π/2)^2=24.674
solved for ∑U= mgh-24.674= 34.861
solved for ω
ω=3.59rad/s
actual answer: 4.9rad/s
What am I doing wrong?