yazz912
- 45
- 0
1. The problem statement, all variables and given/known
A crazed ostrich names rhomboid runs along a mountain path with coordinates given by
r(t) = < e^t, e^-t, sqrt(2) t>
B) what is the change in rhomboids altitude from t=0 to t= 10
C) what is rhomboids speed in x direction when t=4
D) what is rhomboids speed in y direction when t=4
E) find a formula for the total distance traveled by rhomboid from t= 0 to t=4
2. Homework Equations
• integration
•derivatives
3. The Attempt at a Solution
For part b) the first thing I thought to do was to integrate only the z component ( since it's height) and evaluate the integral from 0 to 10? Which I get 50*sqrt(2)
C) for speed in x direction do I take the magnitude of the derivative of e^t then plug t=4?
x'(t) = e^t
||x'(t)|| = e^t
Plug in t=4 I get 54.6
D) I do the same as C) only this time I use the y component ?
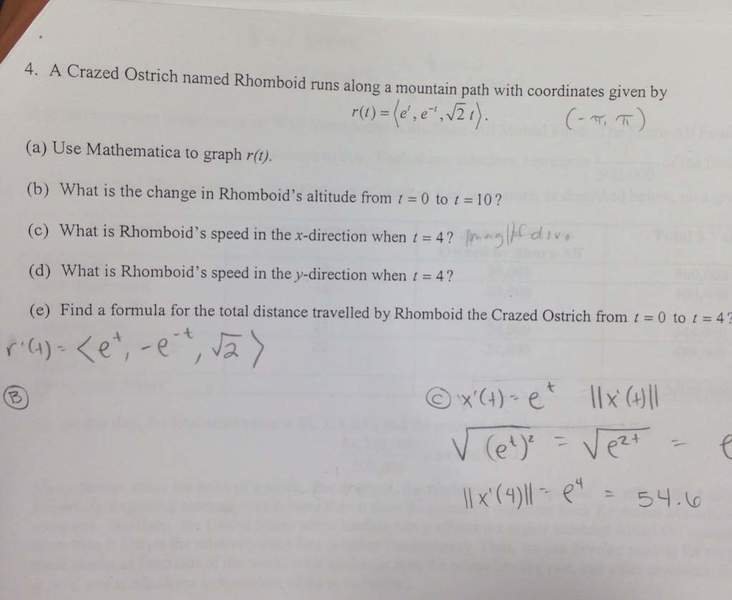
A crazed ostrich names rhomboid runs along a mountain path with coordinates given by
r(t) = < e^t, e^-t, sqrt(2) t>
B) what is the change in rhomboids altitude from t=0 to t= 10
C) what is rhomboids speed in x direction when t=4
D) what is rhomboids speed in y direction when t=4
E) find a formula for the total distance traveled by rhomboid from t= 0 to t=4
2. Homework Equations
• integration
•derivatives
3. The Attempt at a Solution
For part b) the first thing I thought to do was to integrate only the z component ( since it's height) and evaluate the integral from 0 to 10? Which I get 50*sqrt(2)
C) for speed in x direction do I take the magnitude of the derivative of e^t then plug t=4?
x'(t) = e^t
||x'(t)|| = e^t
Plug in t=4 I get 54.6
D) I do the same as C) only this time I use the y component ?