Finding equation of a plane with 3 points

  • Thread starter Thread starter uzman1243
  • Start date Start date
  • Tags Tags
    Plane Points
AI Thread Summary
To find the equation of a plane given three points, the user struggles to arrive at the correct equation, which is 2x + y + 7z = -3. The main issue identified is an incorrect calculation of the cross-product, which is essential for determining the normal vector of the plane. Specifically, the user miscalculated components related to the i and k unit vectors. Clarification on these calculations is requested to identify the exact error. Understanding the correct method for calculating the cross-product is crucial for solving the problem accurately.
uzman1243
Messages
80
Reaction score
1

Homework Statement


attachment.php?attachmentid=68806&stc=1&d=1397897233.png

Homework Equations


N/A

The Attempt at a Solution


attachment.php?attachmentid=68807&stc=1&d=1397897233.jpg


The problem is that I don't get the right answer which is:
2x + y + 7z = -3.

Can you please help me find where I went wrong?
 

Attachments

  • 1.png
    1.png
    3.5 KB · Views: 510
  • IMAG2268.jpg
    IMAG2268.jpg
    15.8 KB · Views: 522
Physics news on Phys.org
Can you explain what you calculated there?
 
uzman1243 said:

Homework Statement


[IMG ]https://www.physicsforums.com/attachment.php?attachmentid=68806&stc=1&d=1397897233[/PLAIN]

Homework Equations


N/A

The Attempt at a Solution


attachment.php?attachmentid=68807&stc=1&d=1397897233.jpg


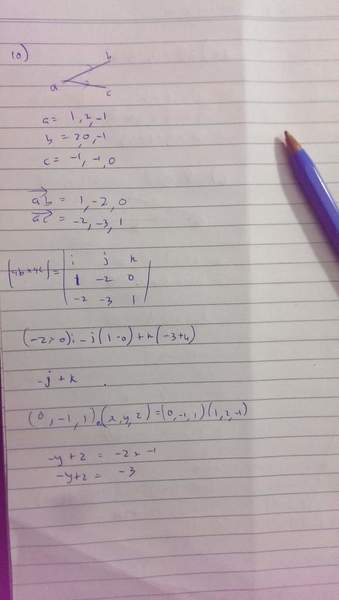
The problem is that I don't get the right answer which is:
2x + y + 7z = -3.

Can you please help me find where I went wrong?
You calculated the cross-product incorrectly.

##\left( -2 + 0 \right)\hat i \ne 0\hat i ##

##\hat k \left( \ (1) (-3) - (-2)(-2)\ \right)\ne \hat k \left(-3 + 4 \right)##
 

Thread 'Family of lines that are at a distance of 5 from the origin'

I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached. The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter. From my side, the only thing I could...
View full post »

Similar threads

Solving Plane Equation 3x + 2y -z = 4
Replies
8
Views
2K
How to Predict Outcomes of New Equations Without Solving for Variables?
Replies
18
Views
3K
Calculating the distance from a point to a plane
Replies
1
Views
2K
Finding the shortest distance from a point to the plane
Replies
7
Views
2K
Find the equation of the plane given point and line (3D)
Replies
2
Views
3K
Find integer points on this equation
Replies
8
Views
1K
Points on a plane satisfying an equation
Replies
2
Views
1K
N lines separate the plane into...
Replies
4
Views
2K
Angle between a plane and a line
Replies
2
Views
2K
Find equation of plane given conditions
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top