jamie_o
- 13
- 0
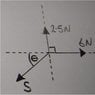
Hello, this isn't technically a homework, but its something I'm trying to figure for myself. As shown in the diagram (in the attachment), there are three forces acting on a particle. The particle is in equilibrium. I have to find the magnitude of S and the angle theta (which ill write as x, because I don't know how to type theta on a computer screen) Now what I would do is solve it horizontally and vertically.
so horizontally: 6 - Scosx = 0
vertically : 2.5 - Ssinx = 0
My problem is where do I go from here? I know I could make it 6 = Scosx and likewise for the other, but it won't help me solve it. Since they are both equal to 0 I tried setting them equal to each other in the hope that the S would cancel and I would get sinx/cosx which is equal to tanx = to a number and then work from there. However I can't get the equation into that form. Any ideas on how I would solve this? Any help is very much appreciated :)
so horizontally: 6 - Scosx = 0
vertically : 2.5 - Ssinx = 0
My problem is where do I go from here? I know I could make it 6 = Scosx and likewise for the other, but it won't help me solve it. Since they are both equal to 0 I tried setting them equal to each other in the hope that the S would cancel and I would get sinx/cosx which is equal to tanx = to a number and then work from there. However I can't get the equation into that form. Any ideas on how I would solve this? Any help is very much appreciated :)