Finding Force on Rope: Trigonometry & Parameters

[Telemachus]

Homework Statement

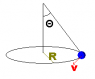
Hi there. Where, I got this exercise. I have a ball attached to an ideal rope with longitude L, moving on a circle with speed V on a circular trajectory with radius R over an horizontal plane.

So it asks me to express the subjected force over the rope as a function of the parameters given on the image below.

So I thought of a_n=\dysplaystyle\frac{v^2}{R}, but the force given by this acceleration isn't the one I'm looking, right? I think I should use some trigonometry to find the projection of the force F=m*a_n over the rope.

What you say?

 

[jhae2.718]

What are the forces acting on the system? What is the net force in the horizontal direction in cases of uniform circular motion? If the ball stays at the same level, what is the net force in the vertical direction?

 

[Telemachus]

I think I get it. In the horizontal direction I got the normal force, right? and in the vertical direction the weight. So the force projected on the rope will be the sum of the weight and the normal force.

Is that right? thanks for your answer.

 

[jhae2.718]

By normal force you're referring to the centripetal force?

The tension in the rope would be the vector sum of the forces in the x and y components. (You could also use Newton's laws to solve for each of the components, and then divide by the appropriate trigonometric function to get the magnitude of this tension force. This would probably lead to a "nicer" looking answer.)

 

[Telemachus]

By normal force you're referring to the centripetal force?

Yes.

The tension in the rope would be the vector sum of the forces in the x and y components. (You could also use Newton's laws to solve for each of the components, and then divide by the appropriate trigonometric function to get the magnitude of this tension force. This would probably lead to a "nicer" looking answer.)

Lets see if I get it: F=m\dysplaystyle\frac{v^2}{R}i-mgj

where i and j are the versors on the direction x and y respectively.
Is that right?

 

[jhae2.718]

That would give you the tension in the rope in vector form, if the positive x direction is taken to be toward the center of the circle.

By the way, you may want to write F as \vec{F} since it's in vector form. (In LaTeX, \hat{\imath} is \hat{\imath} and \hat{\jmath} is \hat{\jmath}.)

 

[Telemachus]

Thank you very much :)