You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
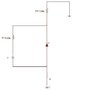
Finding L & C for Circuit Protection: dv/dt & di/dt Values
- Thread starter Johnie
- Start date
-
- Tags
- Circuit Protection
AI Thread Summary
The discussion focuses on determining the appropriate inductance (L) and capacitance (C) values for a circuit protection application involving a thyristor, with specified maximum rates of voltage change (dv/dt) and current change (di/dt). Participants clarify that a snubber circuit is used to protect the thyristor from excessive voltage and current rates, which can lead to unintended conduction or localized heating. The use of Laplace transforms is suggested for analyzing the circuit's behavior, particularly in calculating output voltage and ensuring that chosen L and C values meet the specified di/dt and dv/dt requirements. Additionally, the importance of modeling the thyristor's characteristics, including its on-resistance and parasitic capacitance, is emphasized for accurate analysis. The conversation concludes with suggestions for starting the analysis with basic approximations and considering resonance effects in the circuit.
Engineering news on Phys.org
turin
Homework Helper
- 2,314
- 3
What's a cct? Is that a zener? What is the application of this circuit/what are you trying to protect and where is it connected?
Johnie
- 3
- 0
snubber
cct = circuit
That is a thyristor (scr) (not a zener)
A snubber is used mainly to protect a device from large rates of anode-to-cathode voltage and anode current. If dv/dt for the thyristor is too large, the device will begin to conduct without a gate signal present. If di/dt is too large during turn-on, localized heating will result from the high current density in the region of the gate connection as the current spreads out over the whole junction.
This circuit can be applied to a lot of things -> ie. a buck converter
I know that I can follow the loop from Vcc to ground and determine what (dv/dt)max is using Laplace Transform. To when I'm determining C and L, do have have to pick a value for one (C or L) and then determine the other one ? and then check to ensure di/dt is ok ?
cct = circuit
That is a thyristor (scr) (not a zener)
A snubber is used mainly to protect a device from large rates of anode-to-cathode voltage and anode current. If dv/dt for the thyristor is too large, the device will begin to conduct without a gate signal present. If di/dt is too large during turn-on, localized heating will result from the high current density in the region of the gate connection as the current spreads out over the whole junction.
This circuit can be applied to a lot of things -> ie. a buck converter
I know that I can follow the loop from Vcc to ground and determine what (dv/dt)max is using Laplace Transform. To when I'm determining C and L, do have have to pick a value for one (C or L) and then determine the other one ? and then check to ensure di/dt is ok ?
turin
Homework Helper
- 2,314
- 3
OK, so we're talking about across and through the thyristor, I take it. I am considering the circuit now.
Can the thyristor be modeled as having a threshold voltage and on resistance? Does is have parasitic capacitance (I'm assuming so according to your previous description) and inline inductance? How complicated of a model do you want to use? These issues seem like they would be important. For a first order approximation, I would just replace the thyristor by some typical on resistance value (and perhaps the parasitic cap) and then ensure the ratings are not breached for this resistor.
Why (and how) would you use a Laplace transform to determine a specification that is already given? Can you explain what you mean in more detail?Johnie said:I know that I can follow the loop from Vcc to ground and determine what (dv/dt)max is using Laplace Transform.
Can the thyristor be modeled as having a threshold voltage and on resistance? Does is have parasitic capacitance (I'm assuming so according to your previous description) and inline inductance? How complicated of a model do you want to use? These issues seem like they would be important. For a first order approximation, I would just replace the thyristor by some typical on resistance value (and perhaps the parasitic cap) and then ensure the ratings are not breached for this resistor.
Last edited:
Johnie
- 3
- 0
snubber
I thought I'd look at the dv/dt ratio when the thyristor is off (immediately after). In this case I can follow the loop from Vcc to ground and use Laplace to determine V(output) -> dV(output)/dt. From this I was thinking that I would pick a value for either L or C and calculate the other one that I didn't choose. Then I'd do the same thing for the current (di/dt), when the thyristor is turning on and make sure that these values of L and C satisfy this parameter.
Another thing that I was thinking was that when the thyristor turns off...the inductor and the capacitor might go into resonance ?
I thought I'd look at the dv/dt ratio when the thyristor is off (immediately after). In this case I can follow the loop from Vcc to ground and use Laplace to determine V(output) -> dV(output)/dt. From this I was thinking that I would pick a value for either L or C and calculate the other one that I didn't choose. Then I'd do the same thing for the current (di/dt), when the thyristor is turning on and make sure that these values of L and C satisfy this parameter.
Another thing that I was thinking was that when the thyristor turns off...the inductor and the capacitor might go into resonance ?
turin
Homework Helper
- 2,314
- 3
OK, that sounds pretty good. But it seems like you still need some sort of a model for your thyristor, because you're going to need to know what the state of the circuit is immediately before you "open" the path through the thyristor.
Consider the on-steady-state and a strictly on-resistance model for the thyristor:
There will be an initial current through the inductor given by IL,0 = 120V/(Rthyristor + 1Ω).
There will be an initial voltage across the capacitor given by VC,0 = IL,0Rthyristor.
When the thyristor is switched off, this current IL,0 must go into the cap.
I would start my analysis there, and then increase the order of approximation by including a parasitic cap on the thyristor if you get bored. I imagine that should be good enough, since these values don't really seem to be critical operational values. In fact, if your #1 concern is that the max specs must absolutely not be breached, then just get the largest L and largest C that you can.
About the resonance, I imagine that's why there's a res in parallel with the cap.
Consider the on-steady-state and a strictly on-resistance model for the thyristor:
There will be an initial current through the inductor given by IL,0 = 120V/(Rthyristor + 1Ω).
There will be an initial voltage across the capacitor given by VC,0 = IL,0Rthyristor.
When the thyristor is switched off, this current IL,0 must go into the cap.
I would start my analysis there, and then increase the order of approximation by including a parasitic cap on the thyristor if you get bored. I imagine that should be good enough, since these values don't really seem to be critical operational values. In fact, if your #1 concern is that the max specs must absolutely not be breached, then just get the largest L and largest C that you can.
About the resonance, I imagine that's why there's a res in parallel with the cap.
Very basic question. Consider a 3-terminal device with terminals say A,B,C. Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) establish two relationships between the 3 currents entering the terminals and the 3 terminal's voltage pairs respectively.
So we have 2 equations in 6 unknowns. To proceed further we need two more (independent) equations in order to solve the circuit the 3-terminal device is connected to (basically one treats such a device as an unbalanced two-port...
suppose you have two capacitors with a 0.1 Farad value and 12 VDC rating. label these as A and B. label the terminals of each as 1 and 2. you also have a voltmeter with a 40 volt linear range for DC. you also have a 9 volt DC power supply fed by mains. you charge each capacitor to 9 volts with terminal 1 being - (negative) and terminal 2 being + (positive). you connect the voltmeter to terminal A2 and to terminal B1. does it read any voltage? can - of one capacitor discharge + of the...
I recently made a basic simulation of wire antennas and I am not sure if the near field in my simulation is modeled correctly. One of the things that worry me is the fact that sometimes I see in my simulation "movements" in the near field that seems to be faster than the speed of wave propagation I defined (the speed of light in the simulation).
Specifically I see "nodes" of low amplitude in the E field that are quickly "emitted" from the antenna and then slow down as they approach the far...
Similar threads
- Replies
- 3
- Views
- 3K
- Replies
- 4
- Views
- 2K
- Replies
- 4
- Views
- 5K
- Replies
- 12
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 4K
- Replies
- 3
- Views
- 4K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 17
- Views
- 2K
Hot Threads
-
Spain’s power outage
- Started by Guineafowl
- Replies: 59
- Electrical Engineering
-
PVC Induction Heating Coil Design (early thoughts)
- Started by RickDelta
- Replies: 51
- Electrical Engineering
-
Using Latex Code for Circuit Diagrams
- Started by neilparker62
- Replies: 25
- Electrical Engineering
-
What is the difference between a switch leg and a hot leg?
- Started by sevensages
- Replies: 37
- Electrical Engineering
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math