Finding magnitude and directional sense of resultant moment

[ozzolins]

Do I understand correctly that I need to find resultant moment which is measured in N*m units?
1.

​

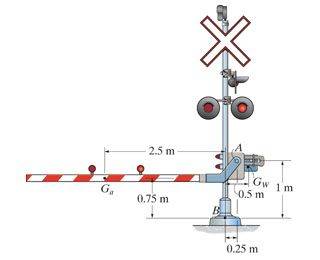The railway crossing gate consists of the 110-kg gate arm having a center of mass at Ga and the 275-kg counterweight having a center of mass at Gw. Determine the magnitude and directional sense of the resultant moment produced by the weights about point B.
2. It's been only a week in university and I'm already struggling with Statics. I'm kind of lost which formula should I use to find required values?
3. I think that it is something like this:

M=-1079.1 (Ga force vector going downwards in y-axis negative direction) * 2.5 - 2697.75 (Gw force vector going downwards in y-axis negative direction) * 0.5 = -4046.63

How wrong am I?

 

[gneill]

Hi ozzolins, Welcome to Physics Forums.

If you are erecting your axes so that the x-y plane lies on the page, then wouldn't Ga have a negative x-coordinate and Gw a positive x-coordinate?

And if the moments are about the point B, then on which coordinate axis does the axis of rotation going through B lie? (around which coordinate axis does the assembly want to rotate?).

 

[ozzolins]

Can you please explain about these coordinates? I'm not sure how to determine whether it's positive or negative. And maybe some example how to solve this exercise?

 

[gneill]

Can you please explain about these coordinates? I'm not sure how to determine whether it's positive or negative. And maybe some example how to solve this exercise?

You've declared the gravitational forces to be acting in the -y direction, so the Y-axis goes up and down the page, with up being positive. Presumably your X-axis is horizontal on the page. This leaves "out" of the page for the Z-axis. Just sketch-in your x and y axes:

So, around which axis does the rotation due to the acting torques "want" to rotate?

You've already got the right idea about the approach. You just need to sort out your axes and directions ("sense").

 

[ozzolins]

I would say around z-axis. I don't know why but I somehow don't see the "big picture" of moments.

Then Ga is positive and Gw in negative, which leads us to:

ƩMo = 110kg*9.81*2.5 - 275kg*9.81*0.5 = 1348.875 N*m = 1.35 kNm ?

 

[gneill]

Yup. That looks good for the rotation axis.

The "sense" of the rotation will be clockwise or counterclockwise about the axis of rotation depending upon the net torque. If you keep track of signs of things through your calculations, the net torque will tell you which direction the rotation will "want" to go.

Sometimes it helps to think of moments or torques in their vector form. If an applied force is described by vector F and the radial vector from the axis of rotation to the point of application of that force is R, then the torque about the axis of rotation is T = R x F. If the resulting torque vector V lies along the +Z direction then the "sense" of the rotation will be counterclockwise.

(This problem could be solved easily using the vector method since you can directly write down the components of all the vectors involved!)

 

[Somewhatsketchy]

Hi... Is the sense of the resultant force to do with whether it is e anti-clockwise or clockwise?