Finding magnitude of vector without direction (kite problem)

[Lorelei42]

Homework Statement

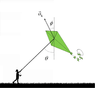
A child is flying a large kite of mass 6.8 kg on a windy day. At the moment shown the tension from the string on the kite has a magnitude of 17.0 N and makes an angle of

= 32.6° from the vertical, and the acceleration of the kite has a magnitude of ak = 7.72 m/s2 and makes an angle of

=37

6° from the vertical as shown in the figure below. The only forces felt by the kite are its own weight, the tension from the string, and a force from the wind.
(picture of problem, shows angles)

Homework Equations

Newton's second Law F(net)=m*a

The Attempt at a Solution

Knowns[/B]: m(kite)=6.8kg, θ(1)=32.6°(vertical angle between y-axis and string), Tension=T(yk)=17N, Φ=37.6°(angle between direction of acceleration and y-axis), a(k)=7.72m/s/s, a(g)=9.81m/s/s
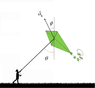
Unknowns: F(wk), θ(2)(angle between wind and y-axis)(see FBD if unclear)

Free Body Diagram:
Free body diagram, apologies for poor handwriting/picture quality)

Equations in Component Form:
X: a*sinΦ*m(k)=F(wk)*sin(θ2)-T(yk)*sin(θ1)
Solved for F(wk) becomes: F(wk)=(a*sinΦ*m(k)+T(yk)*sin(θ1))/sin(θ2)

Y:a*cosΦ*m(k)=F(wk)*cos(θ2)-T(yk)*cos(θ1)-m*g
Solved for F(wk)=(a*cosΦ*m(k)+T(yk)*cos(θ1)+mg)/(cos(θ2))

Solve for θ2
Since both equations are set equal to F(wk) they can be set equal to each other:
(a*cosΦ*m(k)+T(yk)*cos(θ1)+mg)/(cos(θ2))=(a*sinΦ*m(k)+T(yk)*sin(θ1))/sin(θ2)
Add in the given knowns
(7.72*cos(37.6)*6.8+17*cos(32.6)+6.8*9.81)/(cos(θ2))=(7.72*sin(37.6)*6.8+17*sin(32.6))/sin(θ2)
Simplify
122.554/(cos(θ2)=41.189/sin(θ2)
Solve for (θ2)
sin(θ2)/cos(θ2)=41.189/122.554
tan(θ2)=0.336
(θ2)=arctan(.336)=18.57°

Substitute (θ2) back into equation to find F(wk)
xeq. F(wk)=122.554/cos(θ2)=122.554/cos(18.570=129.29N
yeq. F(wk)=41.189/sin(θ2)=41.189/sin(18.57)=129.29N

But apparently this is not the correct answer, so somewhere I went wrong in my process. Any friendly people care to show me where that "somewhere" was.

 

[Lorelei42]

Nevermind, I solved it.

For anyone else who has a similar problem I recommend using a tilted coordinate axis where the positive x direction is parallel to the direction of acceleration.