merzperson
- 30
- 0
*SOLVED*
Figure shows a block of mass m resting on a 20 degree slope. The block has coefficients of friction \mus=0.80 and \muk=0.50 with the surface. It is connected via a massless string over a massless, frictionless pulley to a hanging block of mass 2.0 kg.
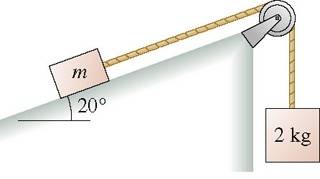
What is the minimum mass m that will stick and not slip?
Fs = \mus * mg
F = ma
The force of the 2kg block on the rope is 2 * 9.8 = 19.6N
Since the m block is not moving, this means that the 2kg block is also not moving, so the force of the rope on the 2kg block is also 19.6N to make the net force 0.
This also means that the force of the rope on m block is 19.6N
I know that there are 3 unknown forces on m block: Earth on the block, normal force, and static friction. The y-component and normal force cancel out so we are left with the x-component of the force of the Earth on the block and the friction force.
mg sin(20) - mg cos(20) * 0.8 = 19.6N
Solve for m. I got m=4.88kg which was wrong. I am lost as to where I might have messed up. It seems like I'm making this problem more complicated than it is.
Homework Statement
Figure shows a block of mass m resting on a 20 degree slope. The block has coefficients of friction \mus=0.80 and \muk=0.50 with the surface. It is connected via a massless string over a massless, frictionless pulley to a hanging block of mass 2.0 kg.
What is the minimum mass m that will stick and not slip?
Homework Equations
Fs = \mus * mg
F = ma
The Attempt at a Solution
The force of the 2kg block on the rope is 2 * 9.8 = 19.6N
Since the m block is not moving, this means that the 2kg block is also not moving, so the force of the rope on the 2kg block is also 19.6N to make the net force 0.
This also means that the force of the rope on m block is 19.6N
I know that there are 3 unknown forces on m block: Earth on the block, normal force, and static friction. The y-component and normal force cancel out so we are left with the x-component of the force of the Earth on the block and the friction force.
mg sin(20) - mg cos(20) * 0.8 = 19.6N
Solve for m. I got m=4.88kg which was wrong. I am lost as to where I might have messed up. It seems like I'm making this problem more complicated than it is.
Last edited: