Dr Zoidburg
- 39
- 0
Homework Statement
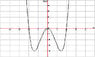
Suppose the graph f''(x) of a function is given by:
(see attachment)
(a) Find all points of inflection of f(x)
The Attempt at a Solution
First I figured, by looking at the graph and seeing the intercept points [(-2,0),(0,0),(2,0)] that f''(x) = x^{4}-4x^{2}
solving for f''(x)=0 gives us x = -2 or 0 or 2.
Between -2 < x < 2 there is no change of sign, which indicates no point of inflection.
Thus the points of inflection for f(x) are at x = -2 and x = 2.
correct?
But how can I find the y intercepts with just what I have? I only know how to find them by putting x back into f(x). As we don't have f(x) here, I'm stuck. Integrating back doesn't help because of the unknown variables.
Or am I trying too hard, and what I've done is the answer?