Finding Rel. Max, Min, and Saddle Points on Levelset

  • Thread starter Thread starter Loppyfoot
  • Start date Start date
  • Tags Tags
    Max Points
Click For Summary
Points A-E on the level sets represent different types of critical points for the function depicted in the diagram. Point B is identified as a relative maximum, while the classifications for points A, C, D, and E remain uncertain. Participants in the discussion express confusion over these classifications and seek clarification on how to determine the nature of each point based on the level sets. The conversation highlights the challenge of visualizing and interpreting level sets in relation to critical points. Overall, the discussion emphasizes the need for a clearer understanding of relative minima, maxima, and saddle points in the context of level sets.
Loppyfoot
Messages
192
Reaction score
0

Homework Statement



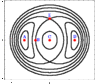
The diagram above represents a collection of level sets for a certain function, where the outer-most level is at the lowest height.

What are points A-E? relative min, relative max, saddle point, or not a critical point


The Attempt at a Solution



I have tried multiple times to get this question right, but I keep failing.

I know that point B is a relative Maximum.
What would C, D , and A be?

Thanks for your help!
 

Attachments

  • cfe9ed6c-b289-4978-a8f9-0188f7166ee5.gif
    cfe9ed6c-b289-4978-a8f9-0188f7166ee5.gif
    6.4 KB · Views: 547
Physics news on Phys.org
Does Anyone have any Ideas? I don't think its that difficult of a question for some, but its just a little bit confusing.
 

Thread 'Distance between a Clock's hands when the distance is increasing most rapidly'

Question: A clock's minute hand has length 4 and its hour hand has length 3. What is the distance between the tips at the moment when it is increasing most rapidly?(Putnam Exam Question) Answer: Making assumption that both the hands moves at constant angular velocities, the answer is ## \sqrt{7} .## But don't you think this assumption is somewhat doubtful and wrong?
View full post »

Similar threads

Finding Local Max and Min values and saddle in mult. Calculu
  • · Replies 1 ·
Replies
1
Views
2K
How do I solve systems of equations to find local max, min, and saddle points?
  • · Replies 2 ·
Replies
2
Views
2K
Quadratic equation to find max and min
  • · Replies 36 ·
2
Replies
36
Views
6K
Finding Saddle point for a function
  • · Replies 6 ·
Replies
6
Views
3K
Local Max/Min and saddle points
  • · Replies 9 ·
Replies
9
Views
6K
Finding local min, max, and saddle points in multivariable calculus
  • · Replies 3 ·
Replies
3
Views
14K
Finding critical points from level curves
  • · Replies 2 ·
Replies
2
Views
8K
Finding Local Min/Max: Second Derivative Test
  • · Replies 3 ·
Replies
3
Views
2K
Classifying Critical Points: Finding Local Extrema and Saddle Points
  • · Replies 2 ·
Replies
2
Views
1K
Understanding Stationary Points: Saddle, Max, or Min?
  • · Replies 2 ·
Replies
2
Views
1K