Finding Resistance of a Voltmeter

AI Thread Summary
To find the internal resistance of a voltmeter, use the formula R = V/I, where V is the emf of the battery (1.50 V) and I is the current (0.212 mA). The resistance Rx is given as 7000 Ohms. The discussion highlights the need for a complete circuit diagram and additional information to accurately determine the voltmeter's resistance. Clarification on the full question is necessary for effective assistance. Understanding these parameters is crucial for solving the problem accurately.
thiefjack
Messages
11
Reaction score
0

Homework Statement


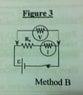
I'm trying to find the internal resistance of a Voltmeter.

The current is 0.212 mA which is measured by I. Rx is 7000 Ohms and the emf of the battery is 1.50 V.

Homework Equations



V = IR so R = V/I

The Attempt at a Solution



How can I start it off to find the Voltmeter's resistance? I don't know exactly to accomplish this. Any help would be appreciated.
 

Attachments

  • photo.JPG
    photo.JPG
    26.1 KB · Views: 511
Physics news on Phys.org
Hi thiefjack! Can you provide the full question? I think you have extracted just part of it for this post. This circuit diagram won't get you anywhere.

Or maybe this circuit is your attempt at an answer?

What information would you need in order to determine the voltmeter's resistance?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Reading of a voltmeter having resistance R across a resistance
Replies
3
Views
2K
Measurement technology textbook problems
Replies
1
Views
541
Measurement technology textbook problems
Replies
2
Views
422
Ammeter and Voltmeter in Series
Replies
11
Views
5K
How Do You Calculate the Resistance of a Voltmeter?
Replies
6
Views
2K
Calculating Internal Resistance: Methods A and B
Replies
13
Views
4K
Find the voltmeter reading in a circuit
Replies
3
Views
15K
Voltmeter problem from (OCR paper) multiple choice
Replies
7
Views
2K
Calculating voltmeter resistance in DC circuit
Replies
4
Views
4K
Reading of a voltmeter and an ammeter
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top